
Generated by Bing Image Creator: Japanese river fall and blue sky and green and red and yellow forests
の続きです。
今回は、前回、前々回で実行した回帰分析を、infer パッケージの枠組みで実行してみます。
Full infer Pipeline Examples • infer の記事を参考にしました。
l_total ~ l_population + l_gdpのモデルを分析してみます。
lm()関数での結果を再度、確認しましょう。
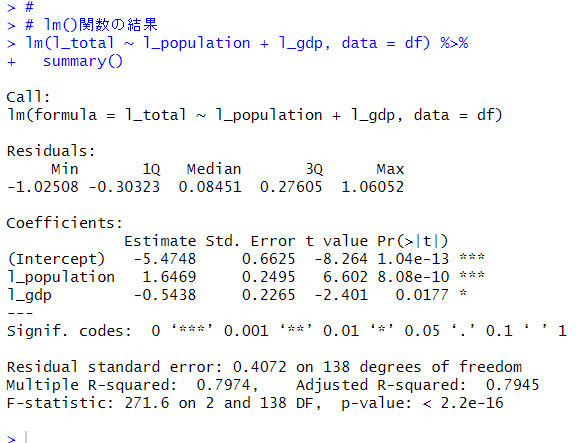
l_populationの係数は、1.6469です。l_gdpの係数は、-0.5438です。どちらもp値は0.05以下なので統計的に有意に0とは違います。
それでは、infer パッケージの読み込みをします。

はじめに、fit() 関数で lm()関数と同じ結果になることを確認します。

specify() 関数でモデル式を設定して、fit() 関数で説明変数の係数を推定します。
l_population の係数は、1.65で、l_gdp の係数は、-0.544となり、lm() 関数と同じ結果であることが確認できました。
次は、被説明変数の l_total と説明変数の l_population と l_gdp の組み合わせをシャッフルしてモデルの係数を推定する作業を1000回繰り返します。

specify() 関数でモデル式を定義した後に、hypothesize() 関数で帰無仮説、(今回は L_total と l_population, l_gdp は独立している) を定義して、generate() 関数で 1000個のシャッフルしたデータフレームを作り、fit() 関数で係数を推定しました。
この、null_dist がどんなものか、ちょっと見てみましょう。
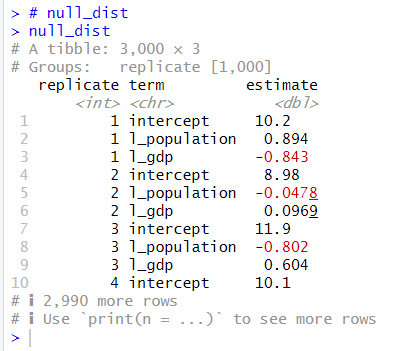
はじめの3行は、replicate が1です。つまり1000個のうちの1個目のシャッフルされたデータからの推計結果で、l_population の係数は、0.894 で、l_gdp の係数は -0.843 でした。2番目のデータからの推計結果は、l_population の係数は -0.0478 で、l_gdp の係数は 0.0969 でした。
visualize() 関数で結果を視覚化してみます。
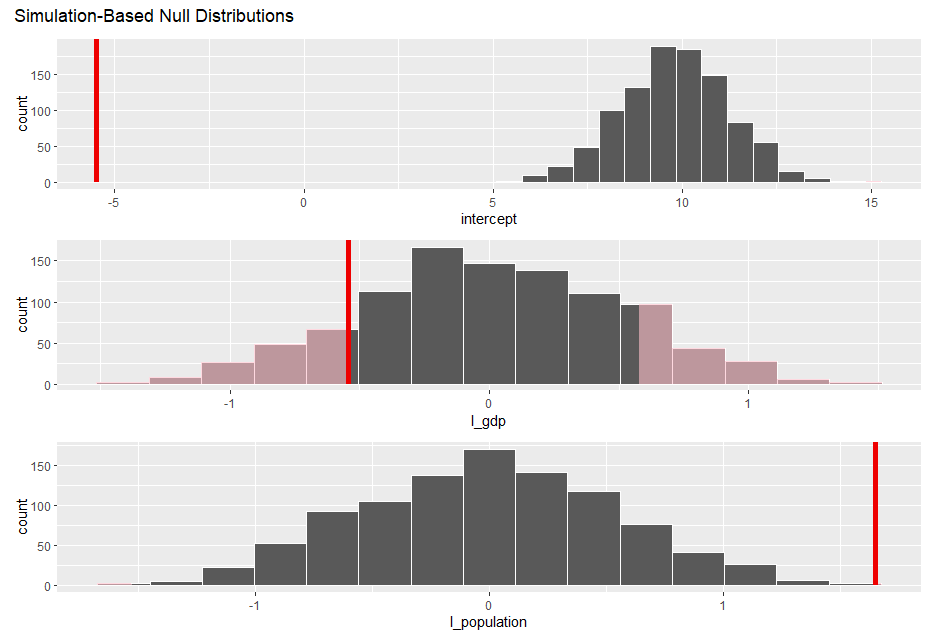
赤い垂直線が、もとのデータから推測された係数の値です。ヒストグラムが、l_total と l_population, l_gdp は関係ない、という帰無仮説のもとで推定された係数の分布です。l_poplulation は明らかに分布から外れていますが、l_gdp は微妙です。
get_p_value() 関数で p値を計算してみます。

l_population の p値は 0 ですが、 l_gdp の p値は 0.262 と0.05 よりも大きくなり、有意な結果ではありません。
lm() 関数と summary() 関数の結果と infer パッケージの枠組み(シミュレーションベース)の結果、どちらが信頼できるかというと、infer パッケージの結果のほうだと思います。lm() 関数と summary() 関数の結果は、方程式ベースで、正しい結果になるためには、いろいろな前提条件、例えば、残差が均一分散で正規分布しているなどが満たされる必要があるからです。
シミュレーションベースのほうは、そのような前提条件はありません。
今回は以上です。
次回は、
です。
初めから読むには、
です。