
UnsplashのKwang Mathurosemontriが撮影した写真
今回は、per_chg: 人口10万人当たりの病院数の変化をper1999: 1999年の人口10万人当たりの病院数と、y1999: 1999年の病院数で回帰分析をしてみましょう。
まずは、lm()関数で回帰分析してみます。

summary()関数で結果を表示します。
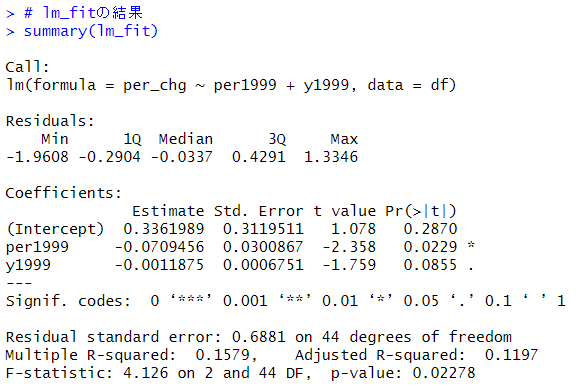
p-value: 0.02278 となっているので、5%の有意水準でこの回帰モデルは有意です。
per1999の係数の符号は、マイナスなので、1999年の人口10万人当たりの病院数が大きいところほど、2019年までの変化幅(減少幅)が大きいということです。p値が0.0229なので、5%の有意水準で有意な結果となっています。
y1999の係数の符号もマイナスです。1999年の病院数が多いところほど、変化幅(減少幅)が大きいということですね。p値は0.0855なので、5%水準では有意ではなくて、10%水準では有意、という結果です。
lm()関数は数式ベース(理論ベース)の回帰分析でした。
次に、inferパッケージで、シミュレーションベースでの回帰分析をしてみます。

inferパッケージのワークフローでは、specify()関数で回帰モデルを特定して、fit()関数でモデルの係数を推計します。
結果を表示してみます。
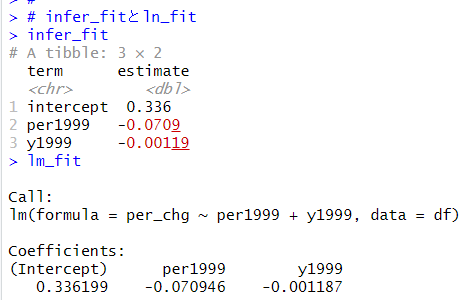
infer_fitの係数とlm_fitの係数が同じであることが確認できます。
線形回帰分析の係数は数式で求まりますので、同じ結果ですね。
信頼区間は、lm()関数とsummary()関数では数式ベースですが、inferパッケージのワークフローでは、シミュレーションベースになります。
まずは、ブートストラップ法で1000回、モデルの係数を推計します。

boot_distを表示させてみます。
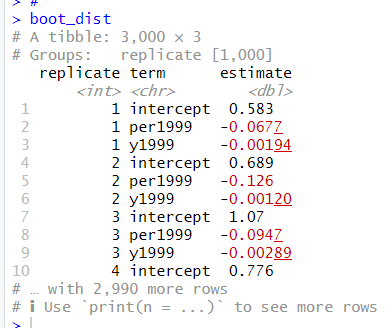
replicateが試行回数の番号です。1回目のブートストラップでは、interceptが0.583, per1999が-0.0677, y1999が-0.00194になったことがわかります。2回目は0.689, -0.126, -0.00120で、3回名は1.07, -0.0947, -0.00289と推計されました。
このブートストラップ法で生成された1000個の推定値から信頼区間を求めます。
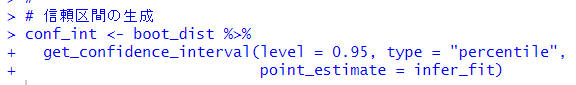
こうして求めたブートストラップ法での信頼区間と理論ベースでの信頼区間を比較してみます。
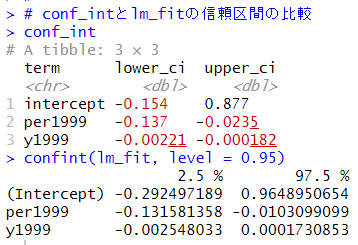
理論ベースでは、y1999の信頼区間は0を含んでいませんので、5%水準では有意ではありませんでしたが、ブートストラップ法では0を含んでいないので、y1999も5%水準でも有意である、という結果になりました。
最後にvisualize()関数でブートストラップ法での信頼区間を視覚化します。

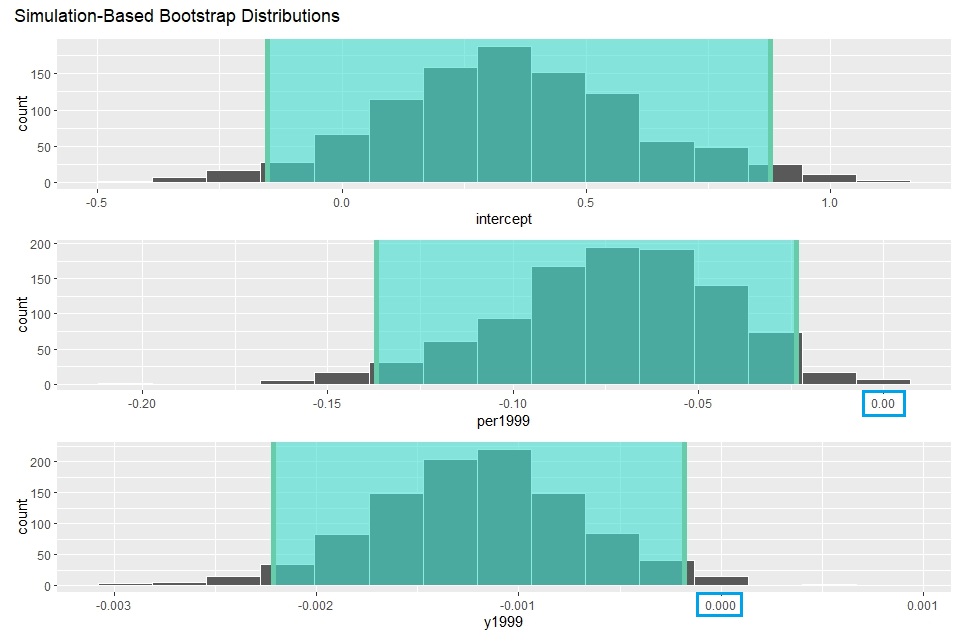
per1999とy1999の信頼区間が0を含んいないことがわかります。

このサイトの一節に以下の文章があります。
Chapter 9 Hypothesis Testing | Statistical Inference via Data Science (moderndive.com)
On the other hand, in most scenarios, the only assumption that needs to be met in the simulation-based method is that the sample is selected at random. Thus, in our experience, we prefer simulation-based methods as they have fewer assumptions, are conceptually easier to understand, and since computing power has recently become easily accessible, they can be run quickly.
シミュレーションベースの信頼区間のほうがいいよ、ってことですね。
今回は以上です。
次回は、
です。
初めから読むには、
です。