の続きです。
前回の分析では、全地域を合計した男性従業者数と女性従業者数の比率が2012年と2016年では変化していて、カイ二乗検定の結果、その変化は統計的に有意なものであること、各地域別では松山都市圏のみ男女比率が増加(男性比率増加)していたこと、がわかりました。
今回は各地域ごとにカイ二乗検定をして男女比率が変化しているのが統計的に有意かどうかを調べてみたいと思います。
地域が14あるので、14の地域についてクロス表を作成してカイ二乗検定をすればいいです。一つ一つクロス表を手作業で作成するのではなく、for関数で自動化してみたいと思います。
まず、クロス表なデータを確認しておきましょう。

男性従業者数は5列目、女性従業者数は6列目です。
札幌のクロス表を[行, 列]のインデックス座標形式で表現するとこうなります。
[1, 5] [1, 6]
[15, 5] [15, 6]
札幌の次の仙台のクロス表はこうなります。
[2, 5] [2, 6]
[16, 5] [16, 6]
札幌と仙台のクロス表の構造を比べると行の値が1増加、列の値は5、6で変化がないことがわかります。なのでこのクロス表の構造は
[i, 5] [i, 6]
[i + 14, 5] [i + 14, 6]
i = 1 ~ 14
という構造になります。
これをR言語のfor関数で再現すればいいわけですね。
具体的にはこうなります。

mという変数にクロス表を格納、mresultという変数にカイ二乗の結果を格納、regionnameという変数に格納して、それらをprint関数で出力します。
それでは結果をみてみましょう。

まずは、札幌、仙台、関東です。赤く記しをつけたところがp値ですが3地域のp値は0.05以下なので統計的に有意な違いが2012年と2016年にある、ということです。

新潟、静岡浜松、中京、近畿の4地域もp値が0.05以下ですので、有意です。

岡山、広島、北九州福岡、熊本の各地域でもp値は0.05以下で有意です。
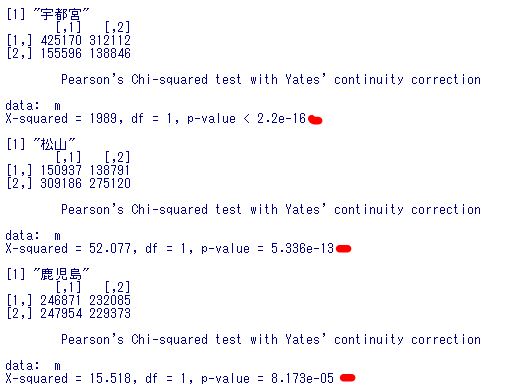
宇都宮、松山、鹿児島の各地域のp値も0.05以下です。松山都市圏の男性比率の増加は有意な増加だったとわかります。
今回は以上です。
次回は
です。