の続きです。
今回はR言語のlm関数を使って、線形単回帰分析の練習をしてみたいと思います。
今まで分析していなかった面積事業所数と面積従業員数の線形単回帰分析をしてみたいと思います。面積事業所というのは、1平方キロメートル当りの事業所数、面積従業員数というのは1平方キロメートル当りの従業員数です。事業所の数が多ければ、従業員の数も多くなるのが予想されます。
これを線形単回帰式で表すと、
面積従業員数 = a + b * 面積事業所数 + 誤差項
という式で表すことができます。この式の場合、面積従業員数が目的変数(従属変数や被説明変数ともいう)と呼ばれます。面積事業所数は説明変数(独立変数ともいう)とも呼ばれます。aは切片、bは係数です。
まず、散布図を描いて本当に、面積従業員数 = a + b * 面積事業所数 + 誤差項 という関係になっているか確認します。plot関数です。

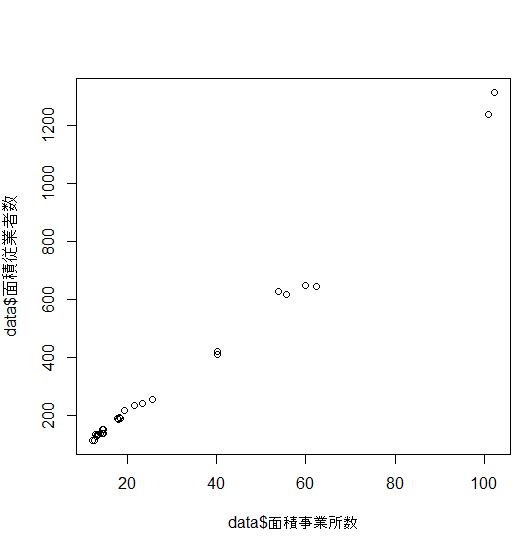
この散布図を見ると確かに線形の関係がありそうですね。
lm関数で線形単回帰モデルを作成し、a(切片)とb(係数)を算出します。
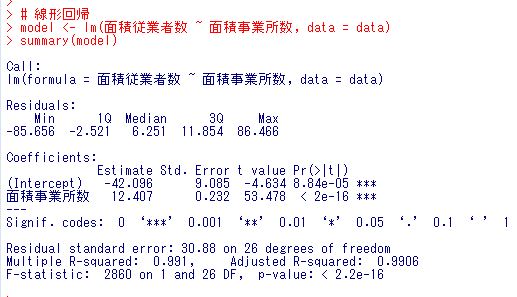
一番下のp-value < 2.2e-16 を見てください。つまり、このモデルは有意だということです。Coefficients: のところが推計された値です。
Interceptが切片で、-42.096 です。
面積従業者数の係数は、12.407 です。
よって推計された回帰式は
面積従業員数 = -42.096 + 12.407 x 面積事業所数 + 誤差項
となります。
plot関数とabline関数で視覚化しましょう。

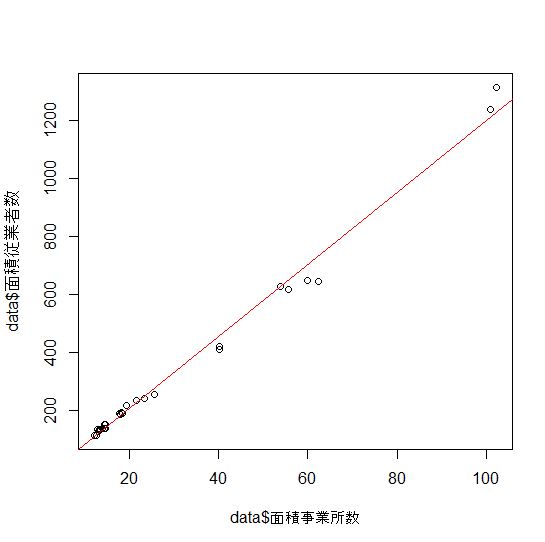
predict関数を使うと、仮定の面積事業所数に対しての面積従業員数が計算できます。ためしに、面積事業所数が15、30、100の3つの値のときの面積従業員数を計算してみます。

このようになります。1平方キロメートル当たりの事業所数が15のときは144人、30のときは330人、100のときは1198人となります。
今回は以上です。
次回は
です。