の続きです。
今回は現状と先行きに統計的に有意な違いがあるのかどうかを調べます。
まずは、summary関数でデータフレームを確認しましょう。

今回もMichael J. CrawleyのStatistics An Introduction Using R Second Edition

Statistics: An Introduction Using R (English Edition)
- 作者:Michael J. Crawley
- 出版社/メーカー: Wiley
- 発売日: 2014/09/23
- メディア: Kindle版
を参考にします。Chapter 6 Two Samplesを主に参考にします。
データフレームのNowが現状で、Nextが先行きです。
Nowの平均値は、6.119です。Nextの平均値は、2.226です。この違いは統計的に有意な違いなのでしょうか?
まず、NowとNextのvarianceが同じと言えるかどうかを見てみます。
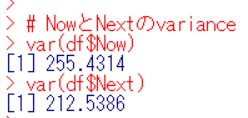
var関数でvarianceがわかります。
Nowのvarianceは、255.4314です。Nextのvarianceは212.5386です。
このvarianceの比、255.4314 / 212.5386をF_ratioという変数名で保存します。

F_ratioは、1.201812です。var関数を使っても手計算でも同じ値です。
このF_ratioが大きい値だとNowとNextのvarianceが違うとわかります。
NowとNextのデータ個数は何個でしょうか?length関数で数えましょう。
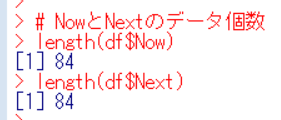
84個ですね。ということは、自由度は、84 - 1 = 83です。
F_ratioの分母も分子も自由度は83です。α = 0.05, 自由度83, 83のときのthe critical value of Fを求めます。qf関数です。

the critical value of Fは1.542242です。F_ratioは1.201812とこれよりも小さいので、NowとNextのvarianceに違いがるとは言えないです。
var.test関数でこれが簡単にできます。

p-value=0.4041と0.05よりも大きいです。つまり帰無仮説:二つのvarianceのratioは1である、を棄却できません。つまり、統計的に有意な違いは無いということです。
では、NowとNextの平均値に有意な違いがあるかどうか、t.test関数でt検定をします。
このケースでは、IndustryがNowとNextを両方回答していますから、対になったサンプルですね。なのでt.test関数にpaired = TRUEを加えます。

p-value=6.704e-07と0.05よりも小さいので、NowとNextの平均値には有意な違いがある、といことです。NowよりもNextのほうが平均値は小さかったですね。(Nowの平均値は、6.119です。Nextの平均値は、2.226です。)、つまり日本企業全体として現状よりも先行きが厳しいとみているのでしょうね。
wilcox.test関数でWilcoxon Rank-Sum Testを実行します。

p-value = 7.986e-07ですので、NowとNextでは有意に違うことがこちらの関数でも確認できました。
今回は以上です。