の続きです。
今回はR言語のlm関数で収入を反応変数、学歴の比率を説明変数にして回帰分析をしてみます。
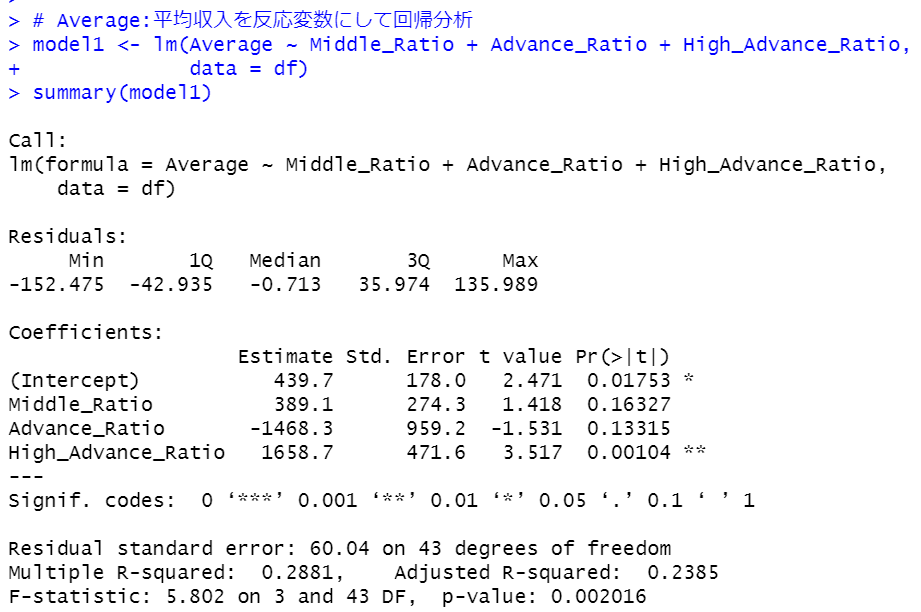
p-value: 0.002016とあります。0.05よりも小さい値ですので、有意なモデルです。
Middle_RatioはPr(>|t|)が0.16327と0.05よりも大きいので有意な変数ではないようです。
削除して、より単純なモデルを作ります。

update関数でモデルを単純化して、anova関数でmodel1とmodel2を比較しています。
Pr(>F)の値が0.1633と0.05よりも大きいです。model1とmodel2では有意な違いはありません。なので、より単純なmodel2のほうが良いモデルです。
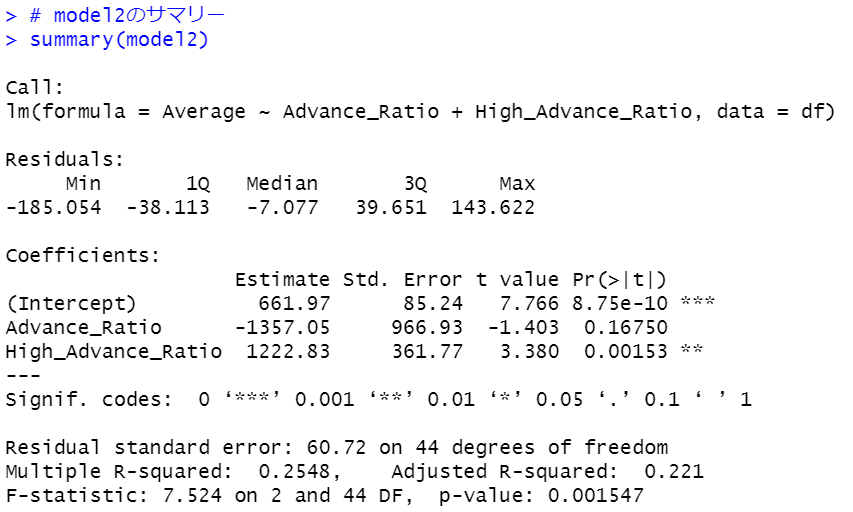
Advamce_Ratioのp値は0.16750と0.05よりも大きいです。これも削除してさらに単純なモデルを作ります。
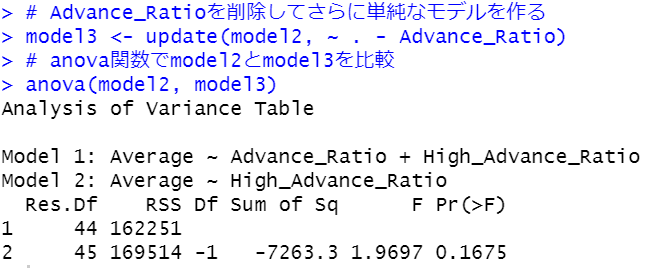
Pr(>F)が0.1675が0.05よりも大きいです。model2とmodel3は有意な違いはありません。
model3を見てみましょう。

p-value:0.000843と0.05よりも小さいですので、有意なモデルです。
平均年収 = 552万 + 830 x 大学・大学院卒の比率
という回帰モデルです。大学・大学院卒の比率が1%上昇すると、平均収入は8万3000円上昇するということですね。
残差プロットを描きます。

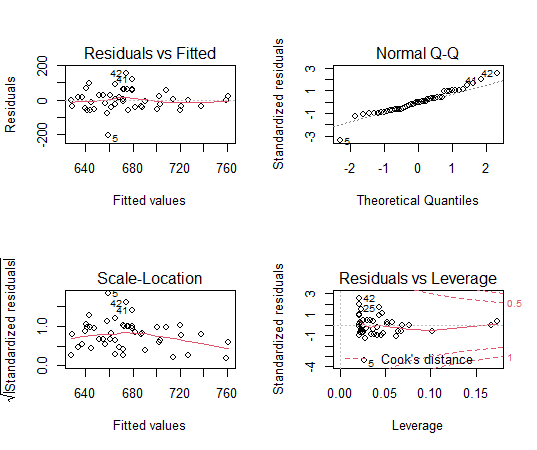
残差は特にパターンになってないようなのでいいと思います。
同じように、Low_Incomeの回帰分析してみます。
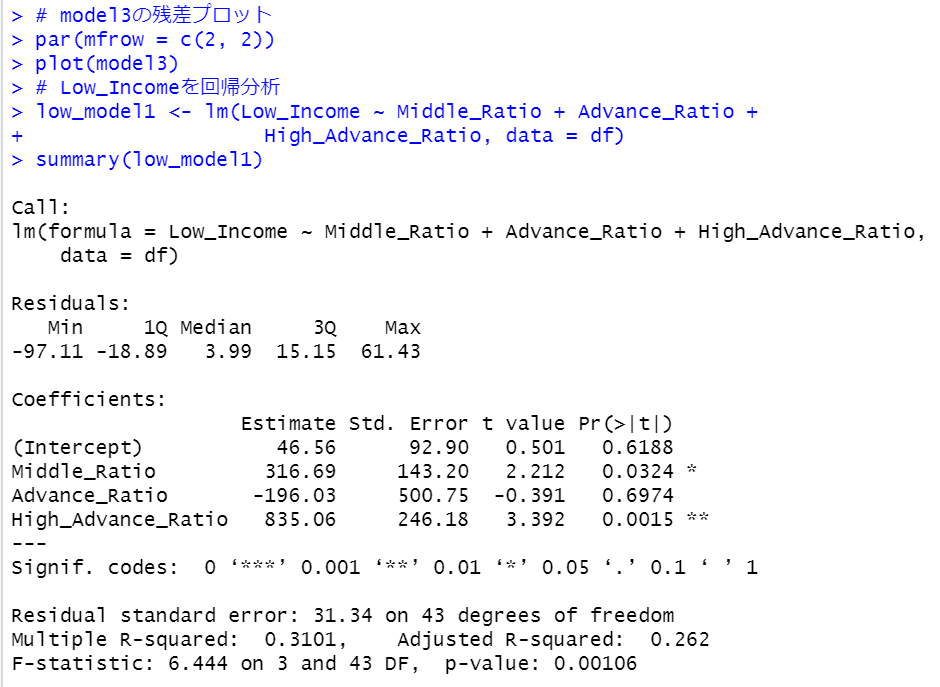
Advance_Ratioを削除してさらに単純なモデルを作ります。

low_model1とlow_model2では有意な違いはありません。low_model2を見てみましょう。
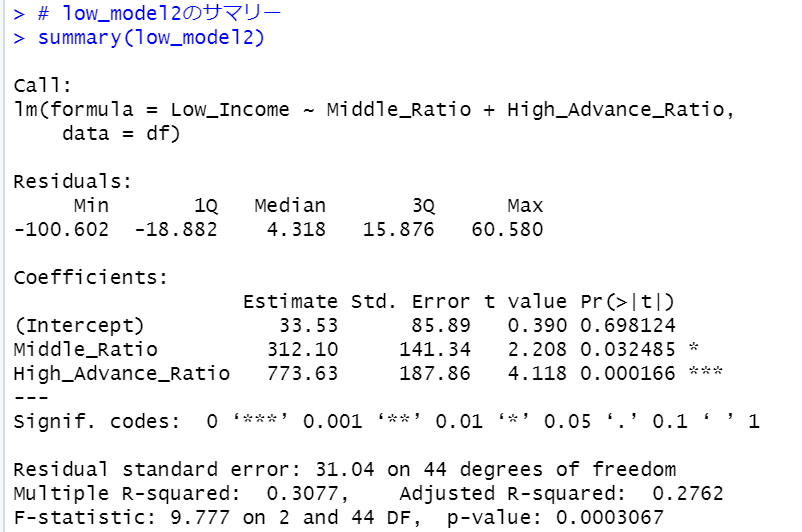
InterceptのPr(>|t|)が0.698124と大きいですね。Interceptを削除してみます。
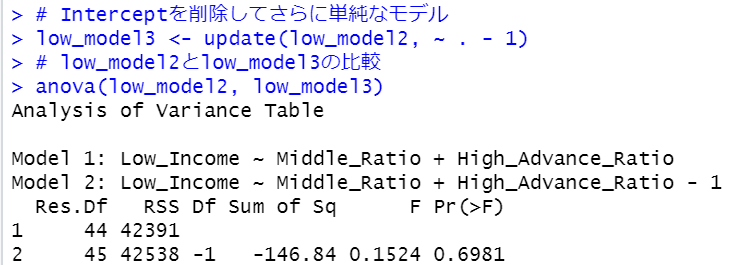
low_model2とlow_model3では有意な違いはありません。
low_model3を見てみましょう。

下位20%の平均収入 = 366 x 高校卒の比率 + 838 x 大学・大学院卒の比率
になります。下位20%の平均収入を上げるには、小学校・中学校卒の比率を減らして高校まで進学できるように、短大・高専卒の比率を減らして大学・大学院卒の比率を高めるといいのでしょうか。
残差プロットを見てみましょう。

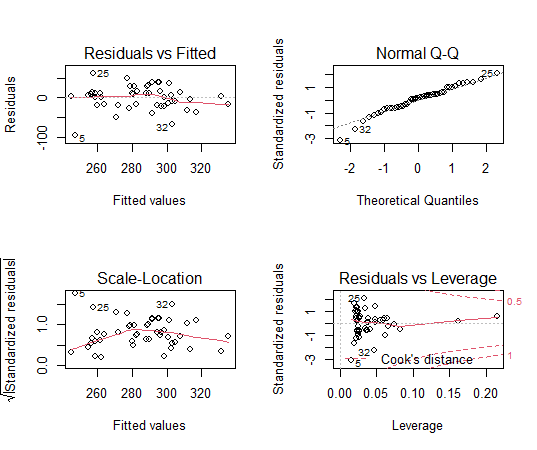
残差プロットは特に問題はないようです。
High_Incomeも同じように回帰分析します。
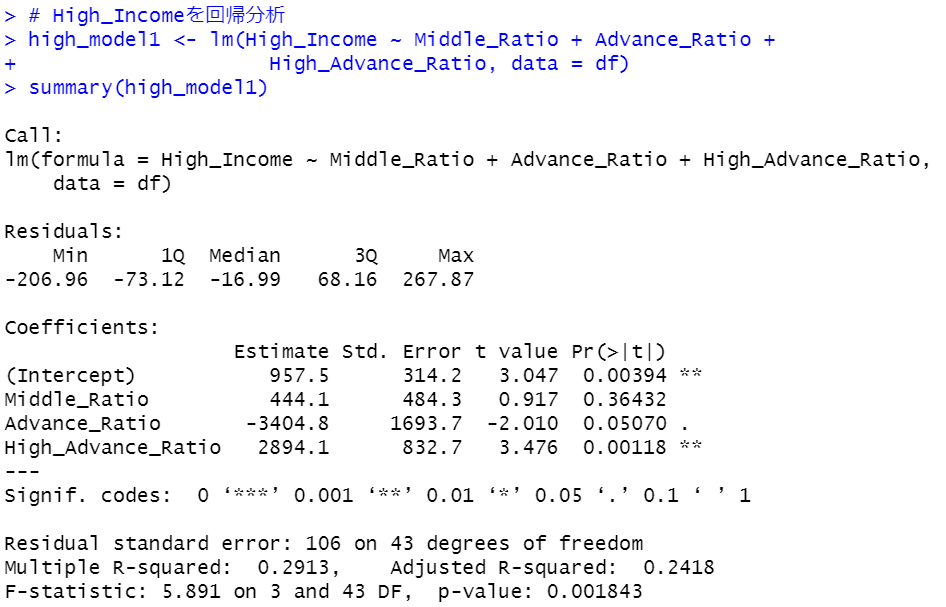
Middle_Ratioを削除します。

Pr(>F)が0.3643と0.05よりも大きいです。high_model1とhigh_model2は有意な違いはありません。high_model2を見てみましょう。
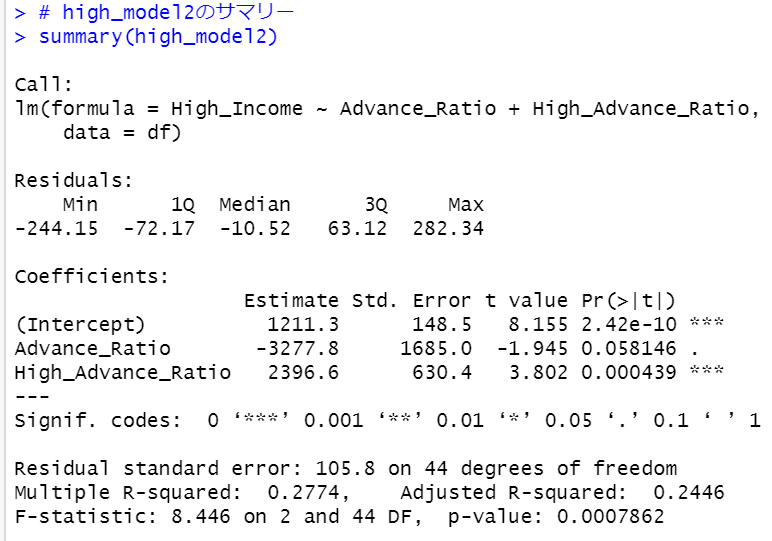
Advance_Ratioを削除してさらに単純なモデルを作ります。
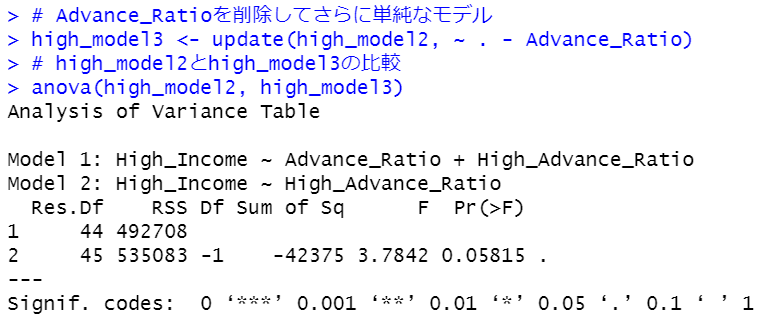
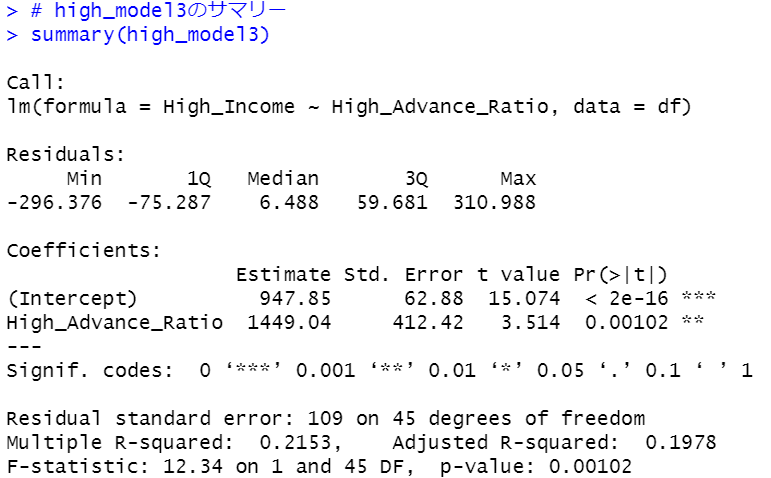
上位20%の平均収入 = 947 + 1449 * 大学・大学院卒の比率
というモデル式です。大学・大学院卒の比率が1%上昇すると、14万円ほど平均収入が上昇します。
残差プロットを見てみましょう。
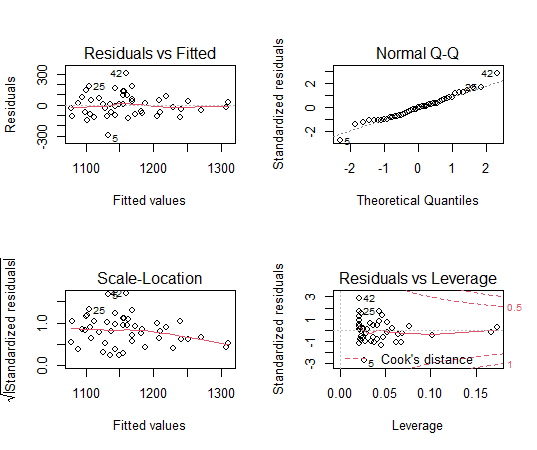
残差プロットは特に問題ないようです。
今回は以上です。
大学・大学院卒の比率が高いほど平均収入は高い傾向がありました。
また、下位20%の平均収入は高校卒の比率も関連があることがわかりました。