の続きです。前回は回帰分析をするつもりが、モンテカルロシミュレーションになってしまいました。
今回は回帰分析をします。
R言語のlm関数です。
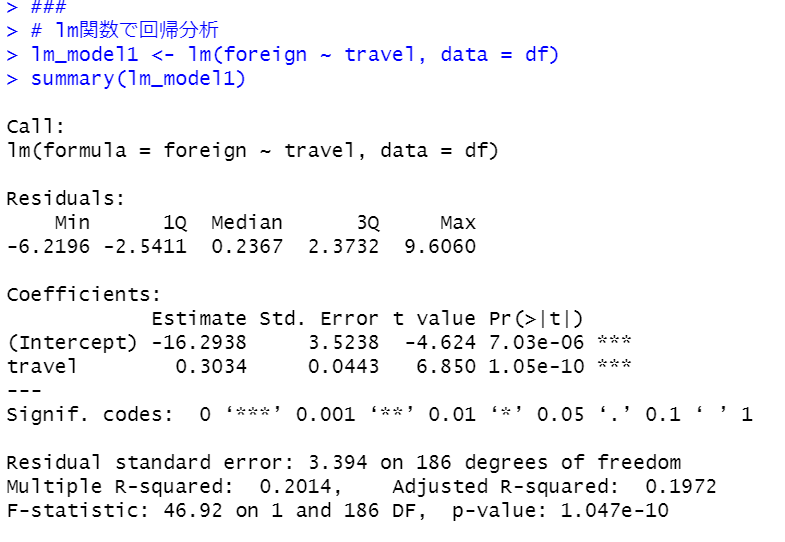
p-valueは1.047e-10なので有意なモデルです。
foreign = -16.2938 + 0.304 x travel というモデルです。
plot関数で残差プロットをみてみましょう。

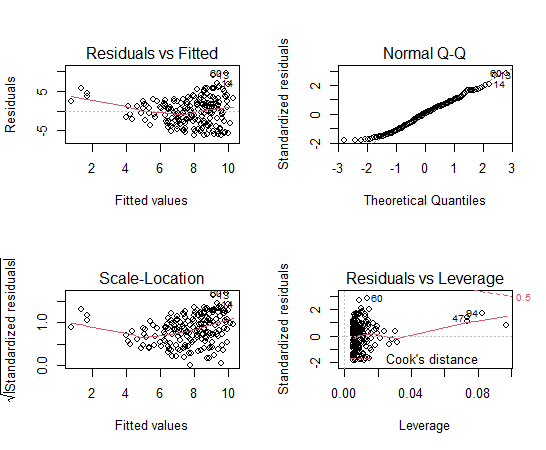
左上のグラフが残差プロットです。Fitted values(横軸)が右にいくほどResidual Valuee(縦軸)のバラツキが大きくなっていますね。これはあまりいいことではないです。
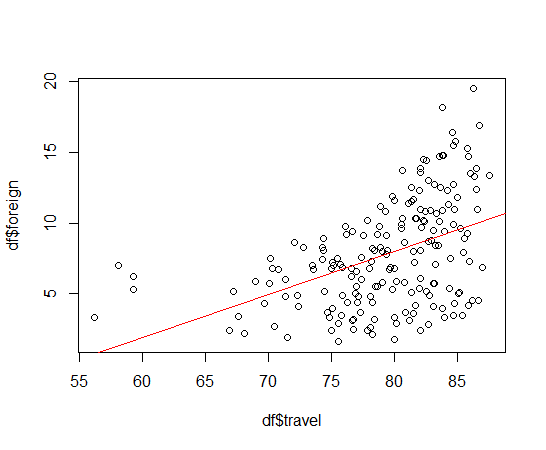
plot関数とabline関数で散布図に回帰直線を重ねてみましょう。

travelの2乗項を追加してみます。
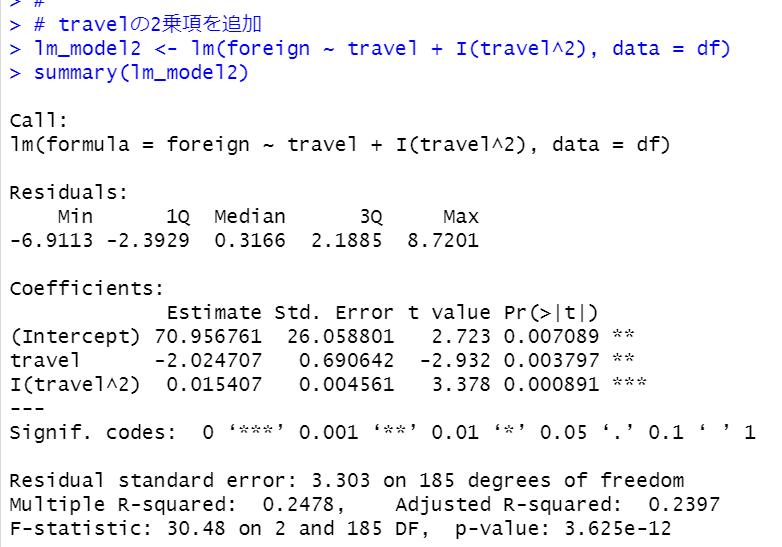
2乗項の係数のp値も0.05以下で有意ですし、モデル全体のp値も3.625e-12と0.05より小さく有意です。
anova関数でlm_model1とlm_model2を比べてみます。
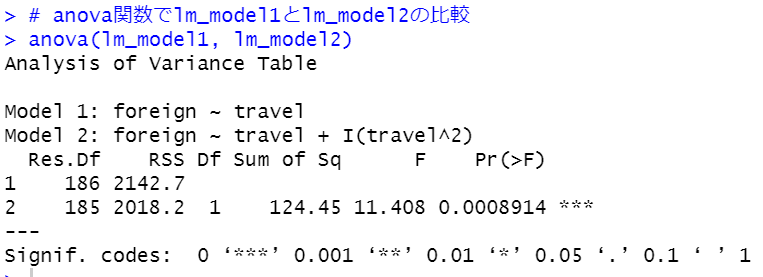
p値が0.0008914と0.05よりも小さいのでlm_model1とlm_model2は有意な違いがあります。
Adjusted R-squaredを見ると、lm_model1は0.1972でlm_model2は0.2397なのでlm_model2のほうがいいですね。
lm_model2は
foreign = 70.956761 - 2.204707 x travel + 0.015407 x tavel^2
という式です。
plot関数とlines関数で散布図とlm_model2の回帰曲線を描いてみましょう。

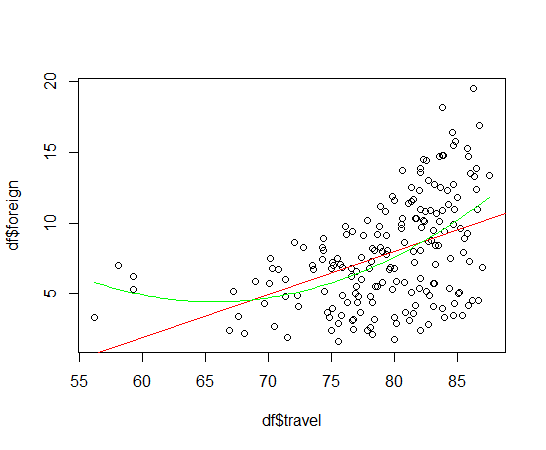
緑がlm_modl2の回帰曲線です。左側のところがより近くなってますね。
plot関数で残差プロットをみてみましょう。
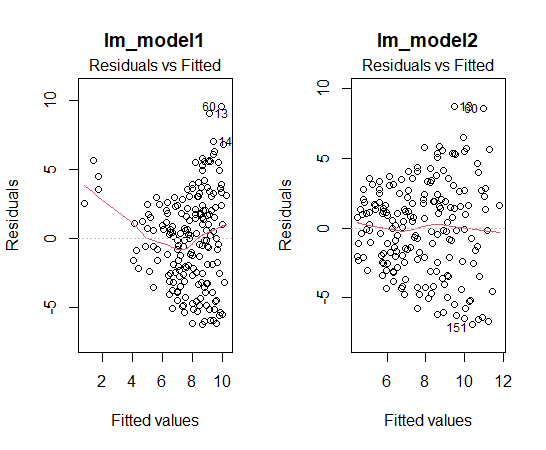
右側のlm_model2の残差プロットのほうが、よりまんべんなく散らばっているのでいいですね。
最後に、yearも加えてみます。
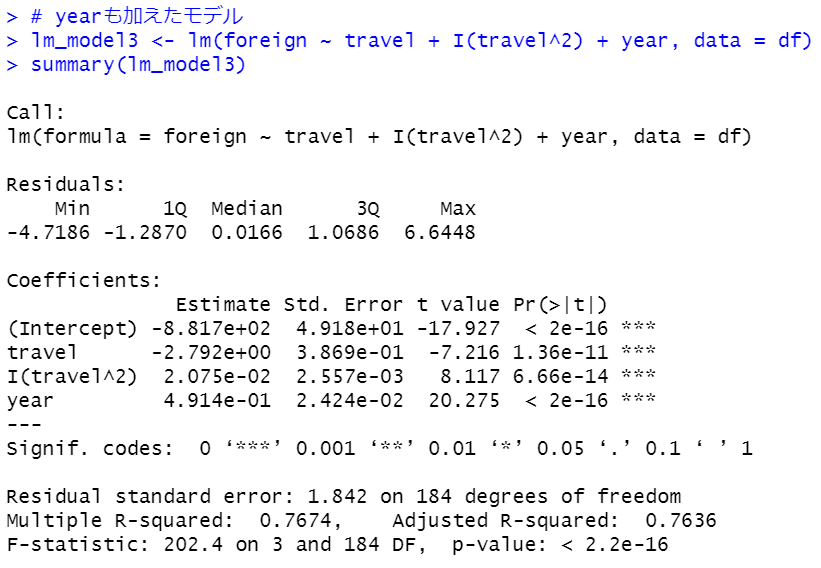
p-value < 2.2e-16と0.o5よりも小さくtravel, travel^2, year全ての係数のp値も0.05より小さいです。Adjusted R-squareも0.7636とlm_model2よりもかなり高くなりました。
anova関数でlm_model2とlm_model3を比較してみます。
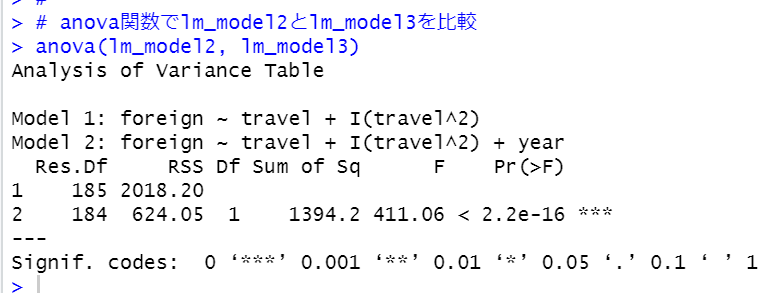
p値が2.2e-16と0.05よりも小さいので、lm_model2とlm_model3は有意に違います。
Adjusted R-squareの大きいlm_model3のほうが良いモデルです。
lm_model3は
foreign = -881.7 -2.792 x travel - 0.02075 x travel^2 + 0.4914 x year
という計算式です。
散布図と回帰曲線を描きます。
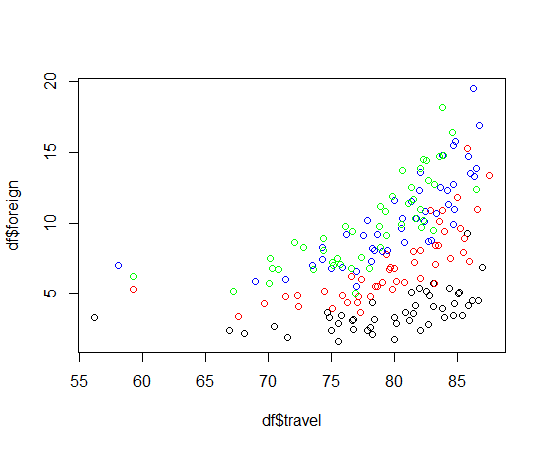
まずは年度ごとに色分けした散布図を描きました。
これにlines関数で回帰曲線を重ねます。

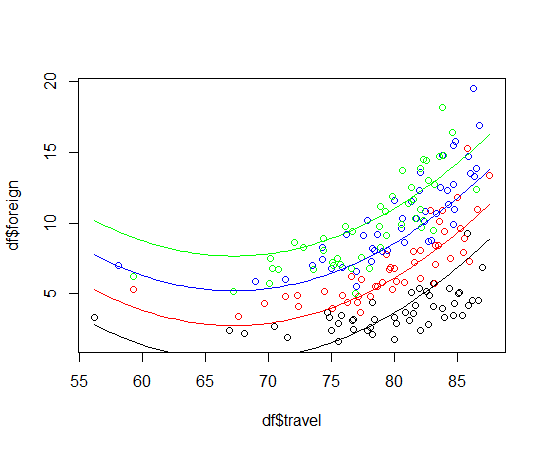
いい感じにフィットしていますね。
残差プロットもみておきましょう。

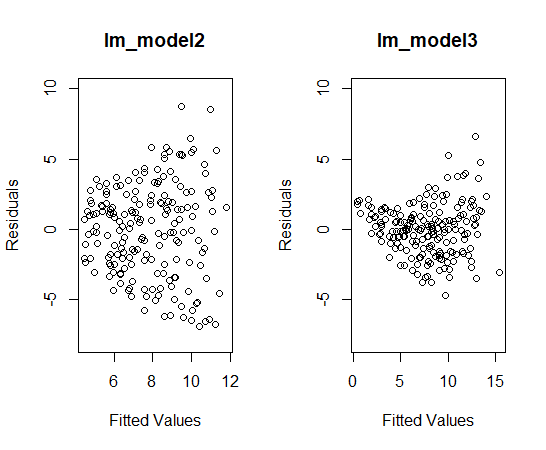
右側のlm_model3のほうが残差が小さいことがわかります。
今回は以上です。
次回は
です。
はじめから読むには、
です。