の続きです。
前回のヒストグラムを見ると、現在貯蓄現在高のジニ係数は2014年度のほうが大きくなっているようでした。
今回はR言語で統計的に有意に違っているのかを検定してみます。
はじめに、group_by関数+summarize関数+mean関数で年度ごとの平均値を見てみます。
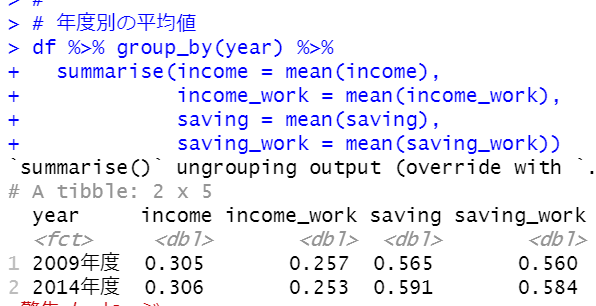
income, income_workはあんまり平均値に差はないようですが、saving, saving_workには差があるようですね。
下準備として、データフレーム、dfを都道府県順に並べておきましょう。
arrange関数を使います。
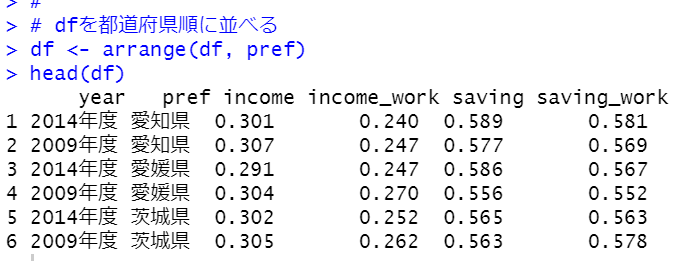
愛知県、愛媛県、茨城県、、と順番に並びました。
平均値を比べるには、まず分散が同じかどうかを確認しないといけません。var.test関数で検定します。

p-value = 0.9094と0.05よりも大きいので、帰無仮説(分散は同じ)を棄却できません。
つまり、2009年度と2014年度でincome(二人以上の世帯の年間収入のジニ係数)の分散は同じとみなして問題ありません。
分散が同じならば、t.test関数で平均値に違いがあるかどうかを検定できます。2009年度の愛知県と2014年度の愛知県、2009年度の愛媛県と2014年度の愛媛県と比較するのでpaired = TRUEにします。

p-value = 0.448と0.05よりも大きいです。帰無仮説(2009年度と2014年度で平均値は同じ)を棄却できません。つまり、incomeは2009年度と2014年度で違いがあるとは言えません。
同じように、income_work(二人以上の勤労者世帯の年間収入のジニ係数)を調べてみます。

p-value = 0.448と0.05よりも大きいですので、分散に違いがあるとは言えません。

p-value = 0.09813と0.05よりも大きいので、2009年度と2014年度で二人以上の勤労者世帯の年間収入のジニ係数に違いがあるとは言えません。
saving(二人以上の世帯の貯蓄現在高のジニ係数)をどうでしょうか?

p-value = 0.448と0.05よりも大きいので、分散に違いがあるとは言えません。
t.test関数で平均値に違いがあるかどうかを検定します。

p-value = 2.16e-11と0.05よりも小さいです。つまり、平均値に違いがあるといえます。
saving_work(二人以上の勤労者世帯の貯蓄現在高のジニ係数)はどうでしょうか?

p-value = 0.5242と0.05よりも大きいので、分散に違いがあるとは言えません。
t.test関数で平均値に違いがあるかどうかを検定します。

p-value = 3.608e-10と0.05よりも小さいので、平均値に違いがあるといえます。
年間収入のジニ係数は2009年度も2014年度も同じような値といえますが、現在貯蓄現在高のジニ係数は2014年度のほうが有意に大きいです。つまり、格差が拡大しています。
稼ぎの格差は拡大していないが、保有の格差は拡大していました。
今回は以上です。