の続きです。
今回はR言語でヒストグラムを描きます。
一番新しい調査年度のデータで描きましょう。
dfの一番新しい調査年度はいつでしょうか?

2018年度です。
2018年度の所定内給与額の分布状況をヒストグラムでみてみます。

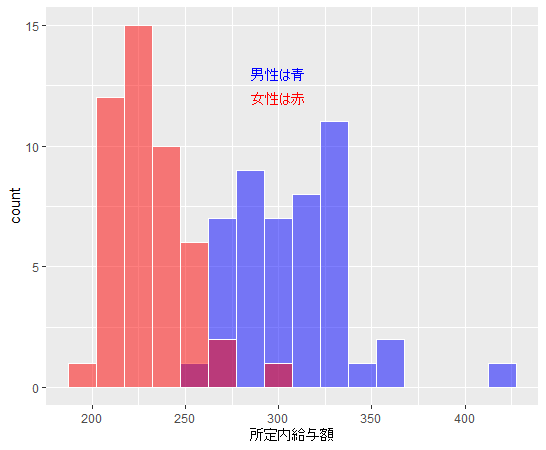
男性のほうが高額ですね。
男女の差が統計的に有意なのかどうか検定してみます。まずは両者の分散が等しいかどうかをvar.test関数で検定します。

p値が0.004846ですので、男性の所定内給与額の分散と女性の所定内給与額の分散は等しいとは言えません。分散が同じではないので、t.test関数ではなくて、wilcox.test関数を使います。

p値は4.191e-16と0.05よりも小さいですので、両者の分布位置が同じという帰無仮説を棄却します。男性と女性では所定内給与額の分布位置はたしかに違うことが確認できました。
次にdf2のデータフレームを使って1日当りの所定内給与額を調べてみます。
まず、df2で一番新しい調査年度を確認します。

2017年度が一番新しい調査年度です。2017年度の1日当りの所定内給与額のヒストグラムを描きます。

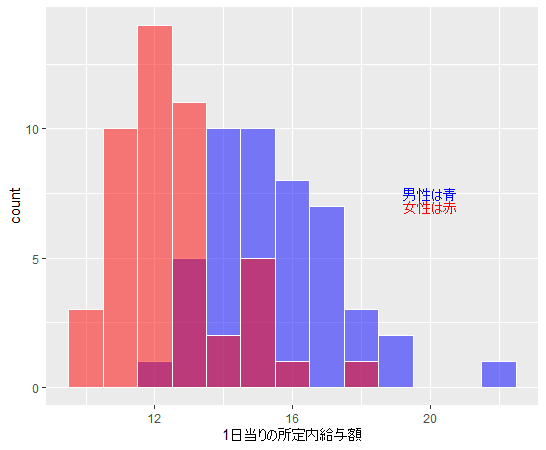
このヒストグラムも男性のほうが高額ですね。
この差が統計的に有意かどうか、検定します。
まず、var.test関数で分散が等しいのかどうかを確認します。

p値が0.3807と0.05よりも大きいので、両者の分散は同じと考えてよいようです。
分散が同じときは、t.test関数で比較できます。

p値が1.805e-11と0.05よりも小さいので、両者の平均値は同じ、という帰無仮説を棄却して、両者の平均値に違いはあるという対立仮説を採用します。
上のt.test関数ではpaired = TRUEを加えていませんでしたが、本当は、東京都の男性の1日当りの所定内給与額、女性の1日当りの所定内給与額とペアになっているデータですので、paired = TRUEを付け加えたほうがより厳密な検定になります。
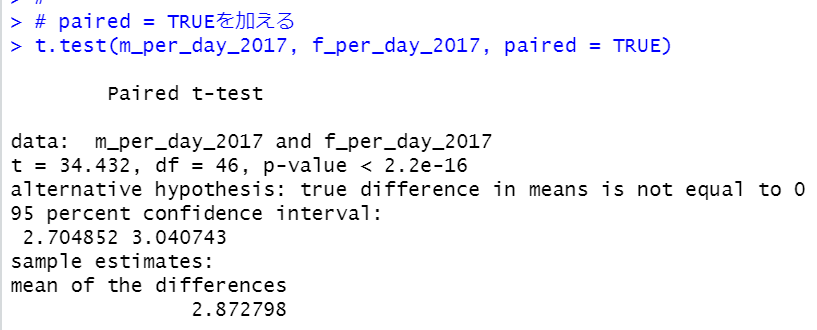
p値が 2.2e-16よりも小さいとさらに小さな値になります。
今回は以上です。
はじめから読むには、
です。