
Photo by Matt Anderson on Unsplash
の続きです。
前回の続きで、今度は交差項を含んだ回帰分析をします。
まずは、per_shobuをincとその他で回帰分析します。

p-valueが1.387e-13とかなり小さいの有意なモデルです。Multiple R-sauaredは0.85とかなりあてはまりが良いです。
Breush-Pegan検定をして誤差項が均一分散かどうかを確認します。

p-valueは0.2003と0.05よりも大きいので、誤差項が均一分散であるという帰無仮説を棄却できません。(つまり、誤差項が均一分散ということです。)
もう一つ、対数変換したper_shobuとincでも交差項を加えて回帰分析してみます。

こちらもp-valueはかなり小さい値で、1%水準で有意なモデルです。
bptest()関数でBreush-Pegan検定をして誤差項が均一分散かを確認します。

p-valueが0.1867と0.05よりも大きいですので、誤差項が均一分散しているといえます。
前回と今回で回帰モデルが4つできました。これらをstargazerパッケージのstargazer関数で見やすい表にして出力します。

まず、stargazerパッケージを読み込みます。
そして、stargazer()関数を使います。
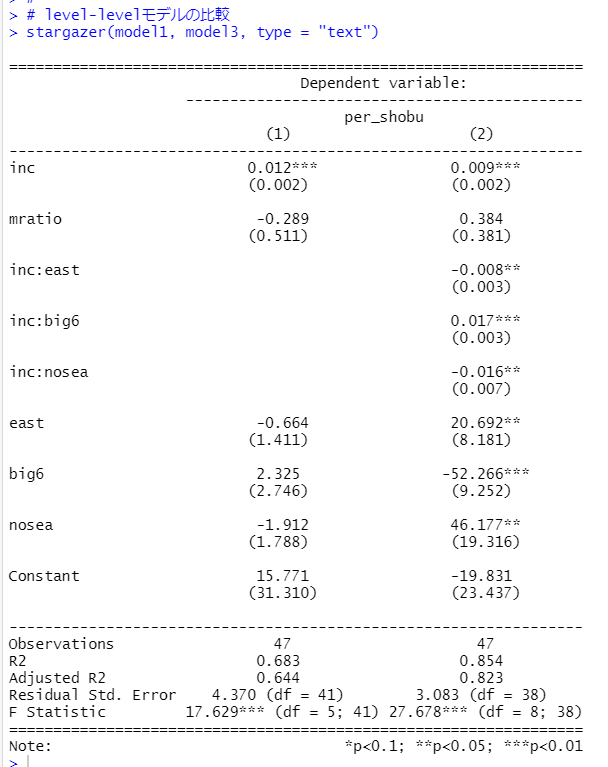
log-logモデルも同じようにします。

4つのモデルを比較すると、model3が一番当てはまりが良いようです。
per_shobu = -19.83 + 0.00916inc + 20.69east -52.27big6 + 46.18nosea + 0.3836mratio - 0.007691inc:east + 0.01670inc:bing6 - 0.01595inc:nosea
というモデルです。
east = 0, big6 = 0, nosea = 0のときは、
per_shobu = -19.84 + 0.00916inc + 0.3836mratioです。inc: 1人当たり県民所得が1千円増えると、per_shobu: 1人当たり書籍・文房具販売額が0.00916千円、つまり9.16円増えます。
今回は以上です。
初めから読むには、
です。