
Photo by Jasper Garratt on Unsplash
HIstDataパッケージのHalleyLifeTableはハレー彗星で有名な、エドモンド・ハレーが調べた年齢と死亡率のデータです。
天文に関することの他にこんなこともしていたのですね。
早速データを呼び出します。

84行、4列のデータフレームです。
age は年齢で、1から84まで、つまち1歳から84歳までのデータです。
deathsは、死亡者数です。
numberは、生存者数です。
ratioは生存率です。number(t+1)/number(t)で計算されています。
それでは、ヘルプのコードを実行します。
はじめは、全体の生存者数をsum()関数で計算しています。

3万3894人でした。
次は、plot()関数で年齢と生存者数をグラフにしています。

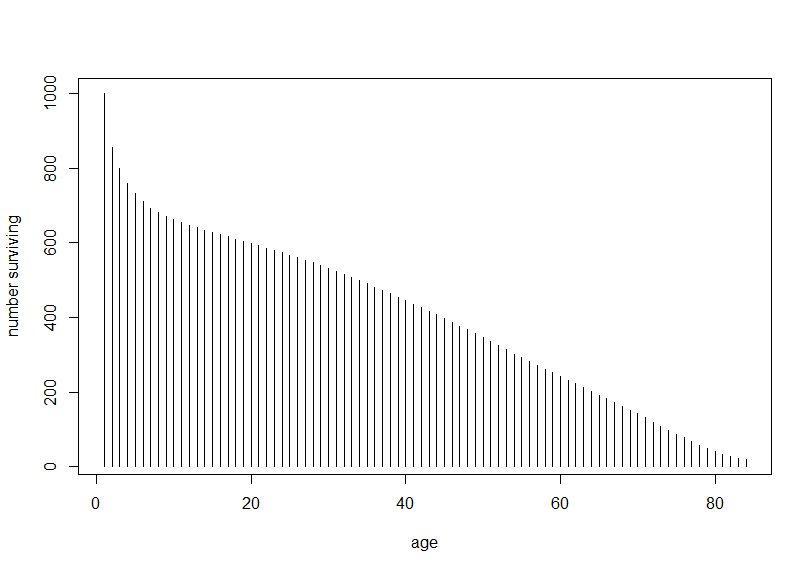
年齢が高くなるほどに生存者数は減少しています。
次のコードはplot()関数で人口ピラミッドを描いています。


segments()関数というのを使って横線を描いています。
次のヘルプのコードは、生存率と年齢のグラフです。

年齢の若い人たち、幼児と年齢の高い人たち、老人の生存率が低いことがわかります。
これでヘルプのコードは終了です。
lm()関数で生存率と年齢の関係を線形回帰してみます。

5乗項まで追加してみました。どの項目の係数も有意な係数です。
この回帰モデルの曲線を先ほどのグラフの上に載せてみましょう。
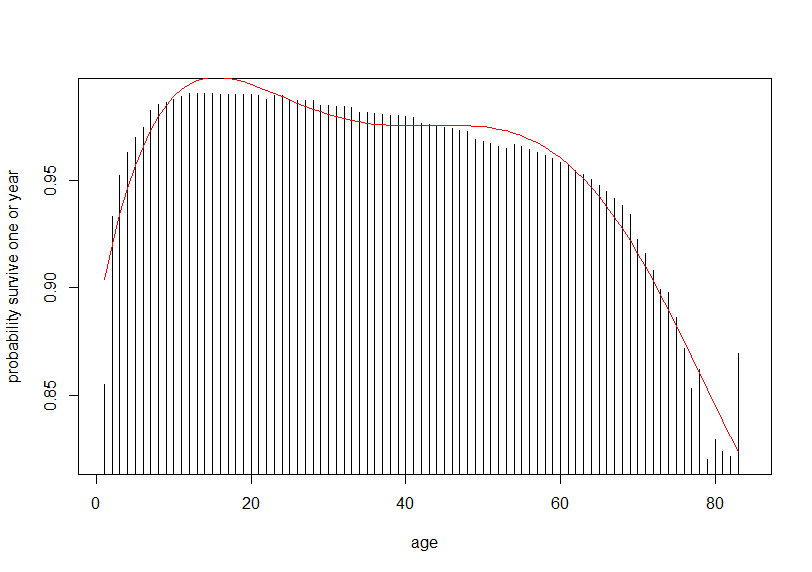
けっこういい感じにフィットしていますね。
下に今回のコードを記載しました。
# 2022-04-24
# HistData_HalleyLifeTable
#
library(HistData)
data("HalleyLifeTable")
#
# str()
str(HalleyLifeTable)
#
# What was the estimated population of Breslau?
sum(HalleyLifeTable$number)
#
# plot survival vs. age
plot(number ~ age, data = HalleyLifeTable, type = "h",
ylab = "number surviving")
#
# population pyramid is transpose of this
plot(age ~ number, data = HalleyLifeTable, type = "l",
xlab = "number surviving")
with(HalleyLifeTable, segments(0, age, number, age, lwd = 2))
#
# conditional probability of survival, one more year
plot(ratio ~ age, data = HalleyLifeTable,
ylab = "probability survive one or year", type = "h")
#
# ratioをageで線形回帰
fit <- lm(ratio ~ age + I(age^2) + I(age^3) + I(age^4) + I(age^5),
data = HalleyLifeTable)
summary(fit)
#
# 回帰曲線をグラフに追加
lines(HalleyLifeTable$age[-84], fitted(fit), col = "red")
#