
UnsplashのJean Girouxが撮影した写真
前回はR言語でヒストグラムを描きました。今回は散布図を描いでみます。

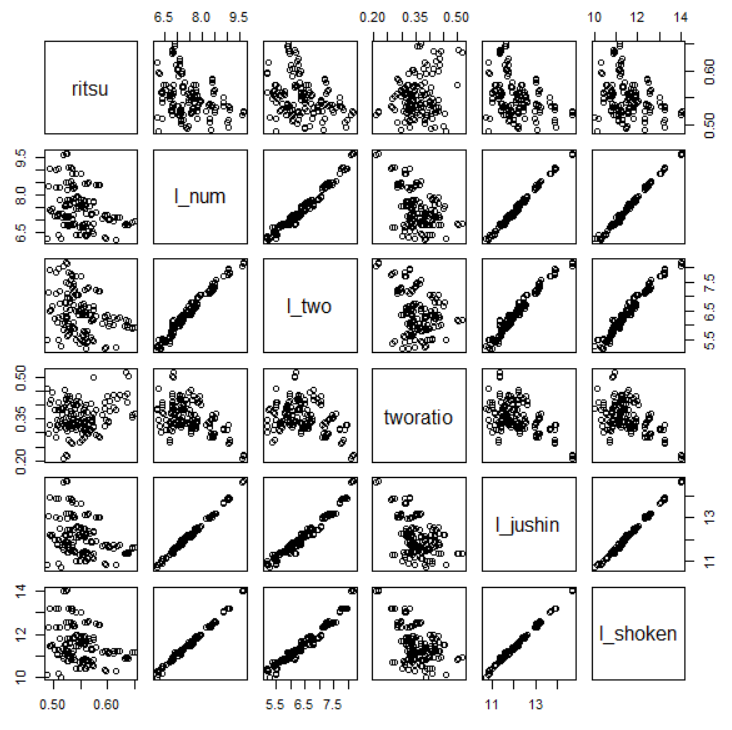
plot()関数で、データフレームの散布図にしたい変数を指定すると、上の画面のような散布図のマトリックスが描かれます。
ritsu: 所見のあった人数の割合と
tworatio: 2回以上実施した事業場数の割合は、どの変数ともあまり相関していないですね。
l_num: 検査実施事業場数の対数変換値、
l_two: 2回以上実施した事業場数の対数変換値、
l_jushin: 受診者数の対数変換値、
l_shoken: 所見のあった人数の対数変換値、
これらの変数は相関していることがわかります。
今度は、X軸を year: 調査年にして散布図を描いてみます。

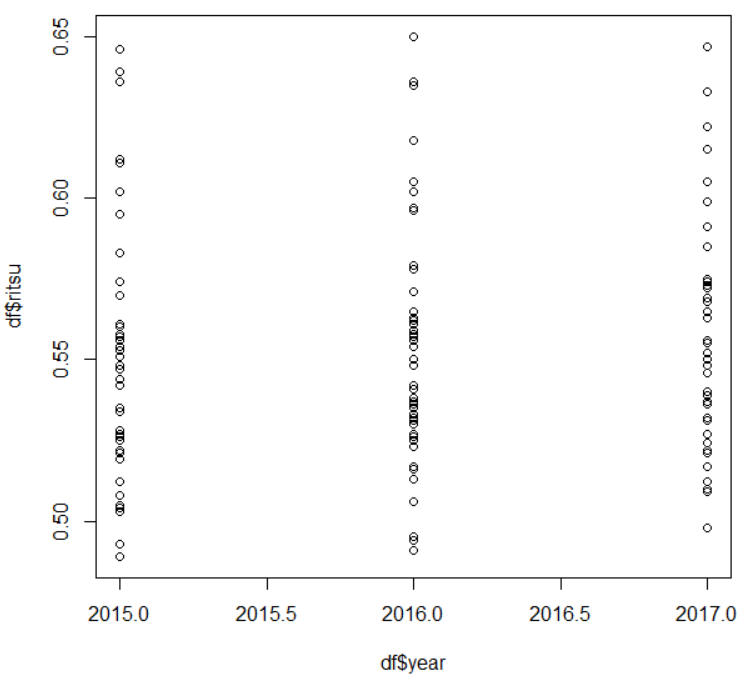
う~ん、傾向がよくわからないですね。。
こういうときは、X軸の year: 調査年をfactor()関数で数値型からファクター型にして、plot()関数を使います。

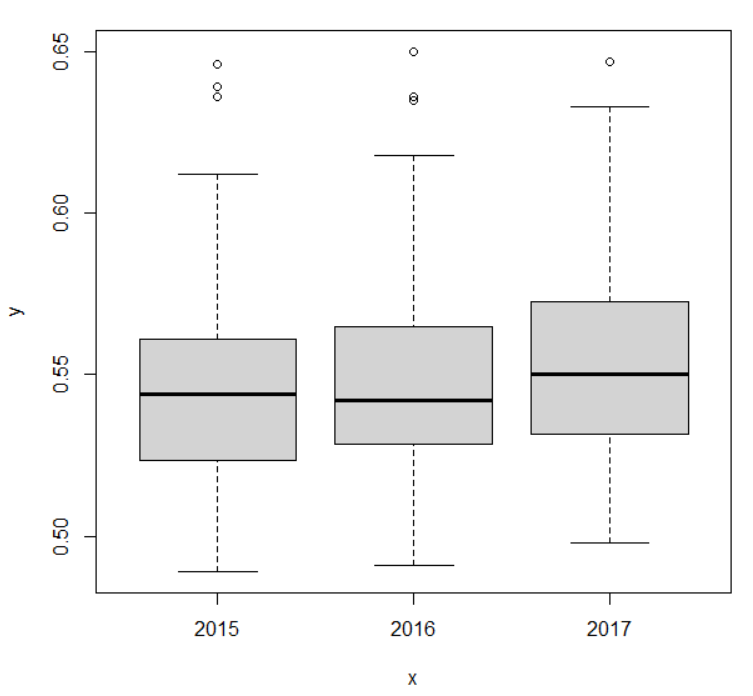
こうすると、year: 調査年ごとに箱ひげ図を描いてくれます。これを見ると、ritsu: 所見のあった割合は、2015年からだんだんと上昇していることが確認できます。
tworatio: 2回以上実施した事業場数の割合も同じように調査年別の箱ひげ図でみてみます。

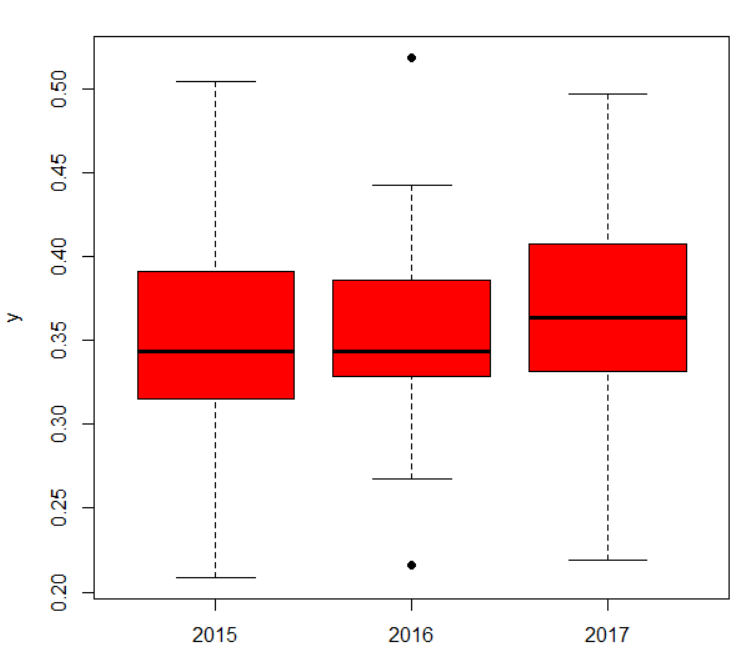
箱ひげ図の真ん中の黒い水平線が中央値の水準です。だんだんと上昇していることがわかりますね。
実際に数値で確認してみましょう。
tapply()関数で、year 別にして、summary()関数で統計値を算出します。
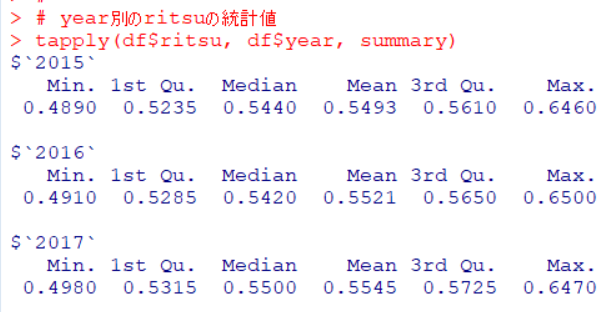
ritsu: 所見のあった割合です。2015年の平均値は0.5493, 2016年の平均値は0.5521, 2017年の平均値は0.5545となっています。
tworatio: 2回以上実施した事業場数の割合も同じようにみてみます。
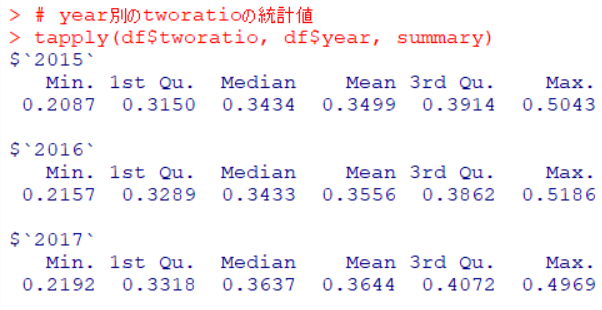
tworatio: 2回以上実施した事業場数の割合は、2015年の平均値は0.3499, 2016年の平均値は0.3556, 2017年の平均値は0.3644です。だんだんと上昇していることが確認できました。
ところで、これら調査年ごとの平均値の違いは統計的に有意な違いと言えるでしょうか?ANOVA分析(ANalysis Of VAriance)で確認します。
aov()関数とsummary()関数を使います。
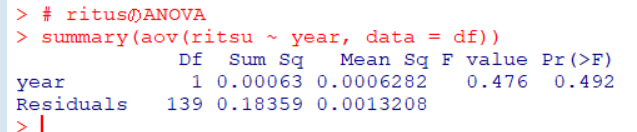
Pr(>F)の数値がp値です。0.492ということなので、調査年ごとにritsu: 所見のあった割合の平均値は違いがあるとは言えないです。
tworatio: 2回以上実施した事業場数の割合はどうでしょうか?
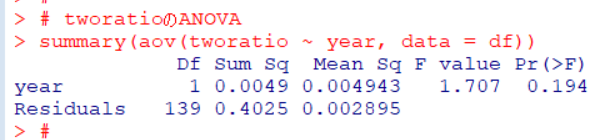
p値が0.194と0.05よりも大きいですから、こちらも調査年ごとに平均値に違いがあるとは言えないです。
ただし、これらのANOVAは都道府県ごとの違いを考慮していないので正しい分析とは言えないです。
pref: 都道府県名も考慮してANOVA分析をしてみます。
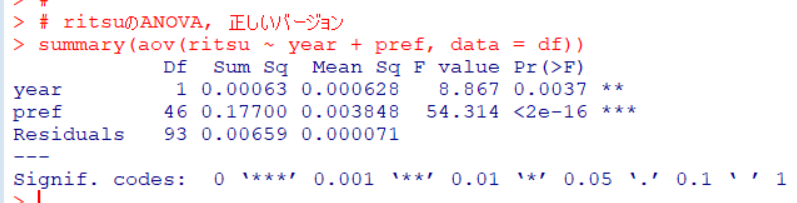
year: 調査年のp値が0.0037と0.05よりも小さくなりました。調査年でritsuの平均値に違いは無い、という帰無仮説は棄却されます。pref: 都道府県名のp値も0.05以下ですから都道府県ごとの違いもあるということですね。
同じようにして、tworatio: 2回以上実施した事業場数の割合も調べてみます。
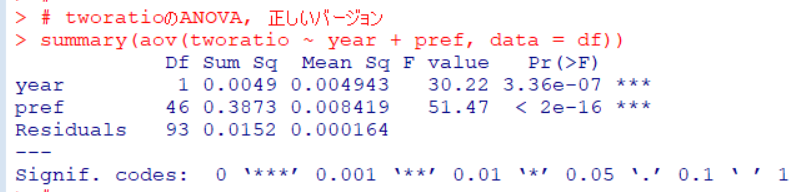
こちらもp値がyear, prefともに0.05以下です。調査年で2回以上実施した事業場数の割合の平均値は違いが無い、という帰無仮説は棄却されました。
今回は以上です。
今回使った関数は、
plot()関数 --- 散布図を描く、X軸がファクター型のときは箱ひげ図になる
factor()関数 --- 変数をファクター型に変換する
tapply()関数 --- 〇〇別に変数を処理する
summary()関数 --- 基本統計量を表示したり、ANOVA分析の結果を表示する
aov()関数 --- ANOVA分析をする
でした。
次回は
です。
初めから読むには、
です。