
UnsplashのGwen Weustinkが撮影した写真
の続きです。
前回はwear_shoeを被説明変数、wariaiを説明変数にして単回帰分析をしました。
今回はもう一つ説明変数を加えてみます。カテゴリーデータを加えてみましょう。
まず、カテゴリーデータを作成します。
nosea: 海が無い県は1、ある県は0というダミー変数からカテゴリー変数を作成します。

mutate()関数の中でifelse()関数とas.factor()関数を使って、no_sea, has_seaという2つの値を取るカテゴリカル変数を作成しました。
glimpse()関数でちゃんとできているか確認します。
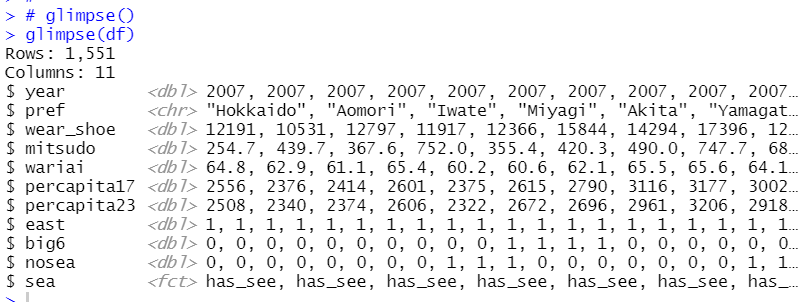
select()関数、pull()関数とtable()関数を使って数を確認します。

has_seaが1287個、no_seaが264個です。
それでは、このseaを説明変数に加えて回帰分析をしてみます。

wariai*sea と * で結んでいるので、このモデルの式は、
wear_shoe = beta0 + beta1*wariai + beta2*sea + beta3*wariai*sea + u
という式です。
結果をget_regression_table()関数でみてみます。

これは、どういう式になるかというと、
seaがno_seaのときは、
wear_shoe = 1800 + 181*wariai -23626 + 380*wariai + u
= -26826 + 561*wariai + u
seaがhas_seaのときは、
wear_shoe = 1800 + 181*wariai + u
ということです。no_seaのときのほうが切片は小さく、傾きは大きいです。
散布図にしてみます。

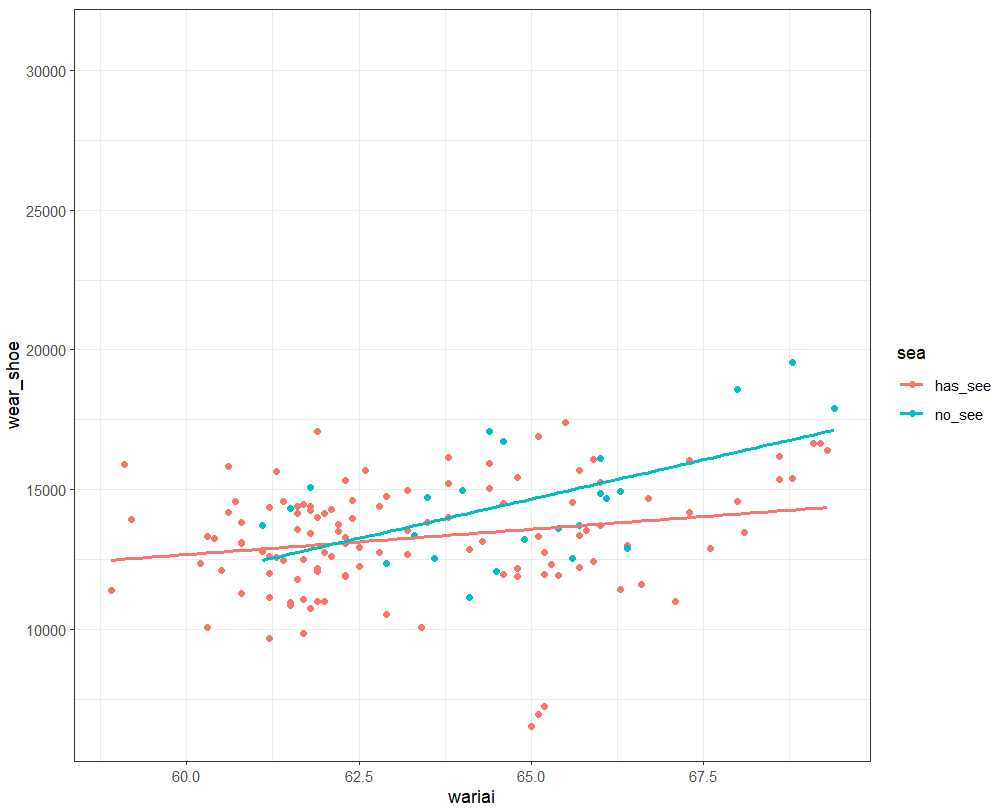
散布図は確かにno_seaの緑色の直線のほうが切片が小さく、傾きは大きいです。
もうひとつ、交差項の無い回帰モデルを分析をしてみます。

こんどは、wariaiとseaを*ではなくて+で結んでいます。
これは、式で表すと、
wear_shoe = beta0 + beta1*wariai + beta2*sea + u
です。
結果みてみます。

式にしてみます。
seaがno_seaのときは、
wear_shoe = -1262 + 230*wariai + 967 + u
= -295 + 230*wariai + u
seaがhas_seaのときは、
wear_shoe = -1262 + 230*wariai + u
です。傾きは230で同じ、切片だけが違います。
moderndiveパッケージのgeom_parallel_slopes()関数をつかって散布図にこの回帰直線を重ねてみます。

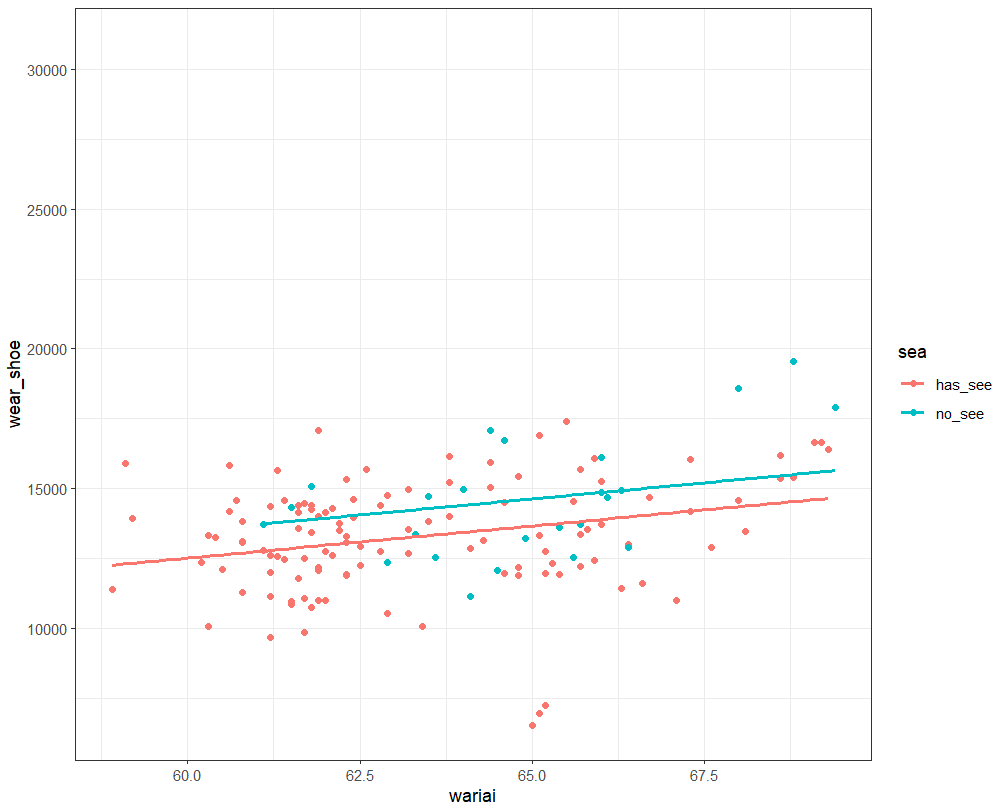
前回の単回帰分析モデルとあわせて3つのモデルを作成しました。
この3つを比較してみます。moderndiveパッケージのget_regression_summaries()関数を使います。
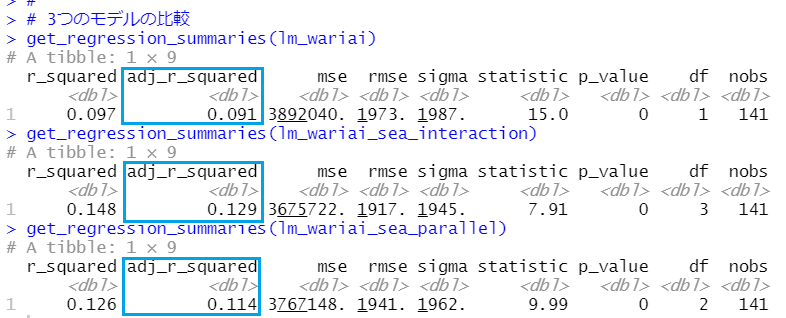
adj_r_squaredの値を比較すると、lm_wariai_interactionモデルが一番、値が大きいです。
この値が大きいほうがよいので、交差項の入ったモデルが一番いいことがわかりました。
今回は以上です。
次回は
です。
初めから読むには、
です。