
UnsplashのSimon Bergerが撮影した写真
の続きです。
今回は、R言語のinferパッケージを使って、opm(営業利益率)の平均値の信頼区間を算出してみます。
まずは、group_by()とsummarize()とmean()を使って、製造業のopm、卸売小売業のopmを確認します。

卸売小売業のopmの平均値は、7.82%で、製造業のopmの平均値は22.7%と確認できます。
では、卸売小売業のopmの信頼区間を算出してみます。
はじめに、ブートストラップ法で平均値を何個も算出します。
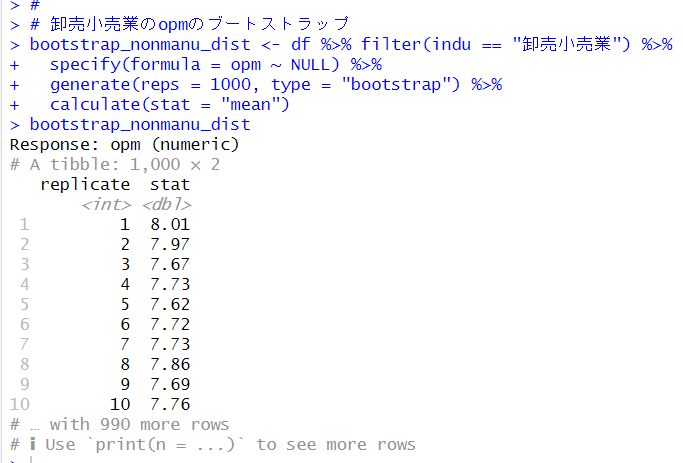
1行目のfilter()関数で、卸売小売業だけにして、
2行目のspecify()関数で、調べたい変数を指定して、
3行目のgenerate()関数で、ブートストラップ法で1000回、サンプルを作っています。
4行目のcalculate()関数で、1000個の平均値を計算しています。
specify(), generate(), calculate()がinferパッケージの関数です。
同じくvisualize()関数で1000個の平均値を視覚化してみます。

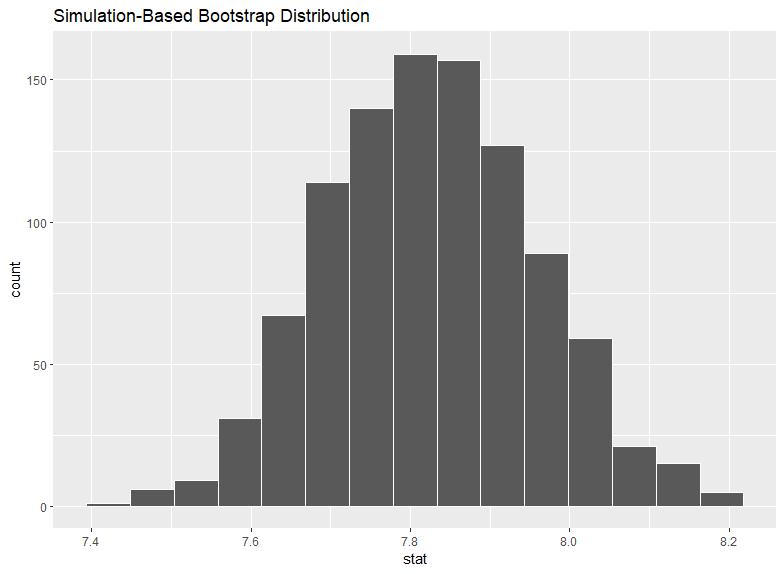
7.82%が事前に計算した平均値ですが、ブートストラップの結果もそのぐらいの値を中心にして分布していることがわかります。
inferパッケージのget_confidence_interval()関数で信頼区間を算出します。
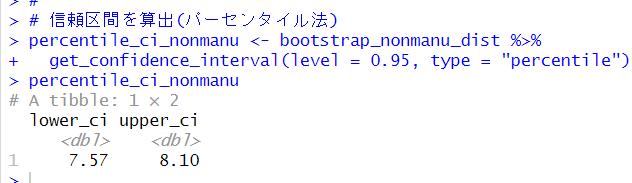
パーセンタイル法の95%信頼区間は、7.57 ~ 8.10となりました。
伝統的な理論ベース(標準誤差を使う方法)での信頼区間もget_confidence_interval()関数で計算できます。
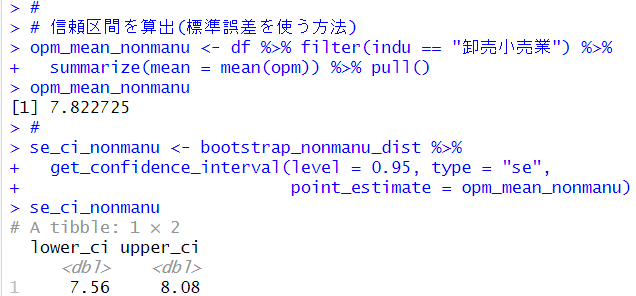
標準誤差を使う方法は、point_estimate, 平均値の値が必要です。95%の信頼区間は7.56 ~ 8.08となりました。パーセンタイル法の信頼区間とほぼ一緒です。
get_confidence_interval()関数を使わないで、教科書どおりの数式でも信頼区間を算出しましょう。

7.55 ~ 8.09となりました。
shade_confidence_interval()関数で信頼区間の範囲をヒストグラムに重ねてみます。

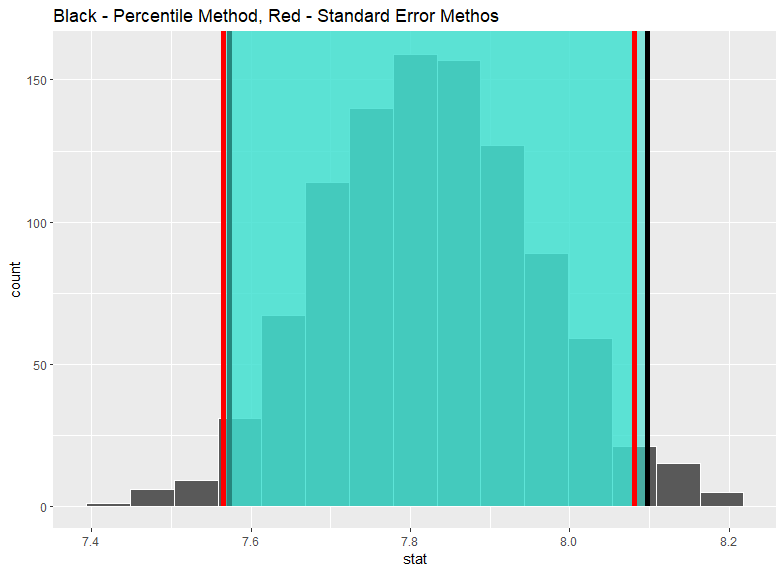
この一連の流れを製造業のopmでもやってみましょう。

specify(), generate(), calcilate()関数でブートストラップ法でサンプルの平均を生成します。
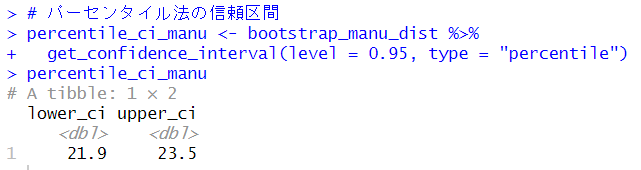
パーセンタイル法の95%信頼区間は、21.9% ~ 23.5%でした。

オリジナルのサンプルの平均値は22.7%でした。

標準誤差を使った95%信頼区間は、21.9% ~ 23.5%でした。

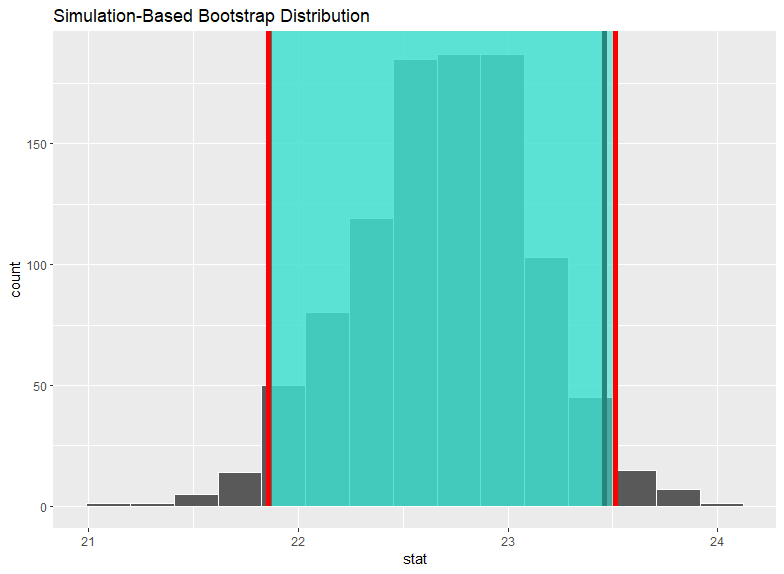
visualized()関数とshade_confidence_interval()関数で視覚化しました。
黒い縦線がパーセンタイル法の信頼区間、赤い縦線が標準誤差を使った信頼区間です。
今回は以上です。
次回は、
です。
初めから読むには、
です。
使用した関数は、
group_by() - グループ化する
summarize() - 平均値などのサマリーを表示
mean() - 平均値を算出
filtet() - データフレームをフィルターする
specify() - 調べたい変数、関係式を指定する
generate() - ブートストラップ法のサンプルを作る
calculate() - 平均などの統計値を計算
visualize() - ブートストラップの結果を視覚化
pull() - データフレームから一つの変数を抜き出す
get_confidence_interval() - 信頼区間を算出
shade_confidence_interval() - ヒストグラムに信頼区間を重ねる。