
Bing Image Creator で生成: Photo, landscape of higher mountains and great fall, a few flowers, white clouds, blue sky
の続きです。前回は箱ひげ図を作成して、生活環境項目 5 項目ごとのデータの分布を見ました。前々回はヒストグラムを作成して、年度ごとのデータの分布を見ました。どちらの切り口でも、大幅に変化している、という印象はありませんでした。
そこで今回からは、生活環境項目については、BOD だけに絞って分析していきましょう。
BOD というのは、ウェブサイトを検索してみると、
BOD (生物化学的酸素要求量) は汚染の元となる有機物の量を間接的に示す水質指標ということです。値が大きいほど、汚染されているということですね。
さっそく、BOD だけのデータフレームを作成します。
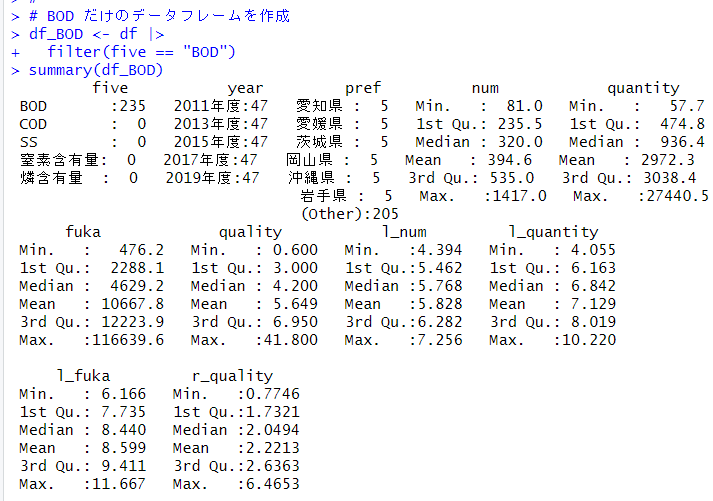
df_BOD の summary() 関数の結果を見ると、
five は必要ない、
quality の最小値が 0 よりも大きいので、対数変換ができる。なので、 r_quality : quality の平方根は必要ない、
とわかります。
df_BOD を手直しします。
l_quality : 平均水質【mg/l】の対数変換値の分布をみてみます。

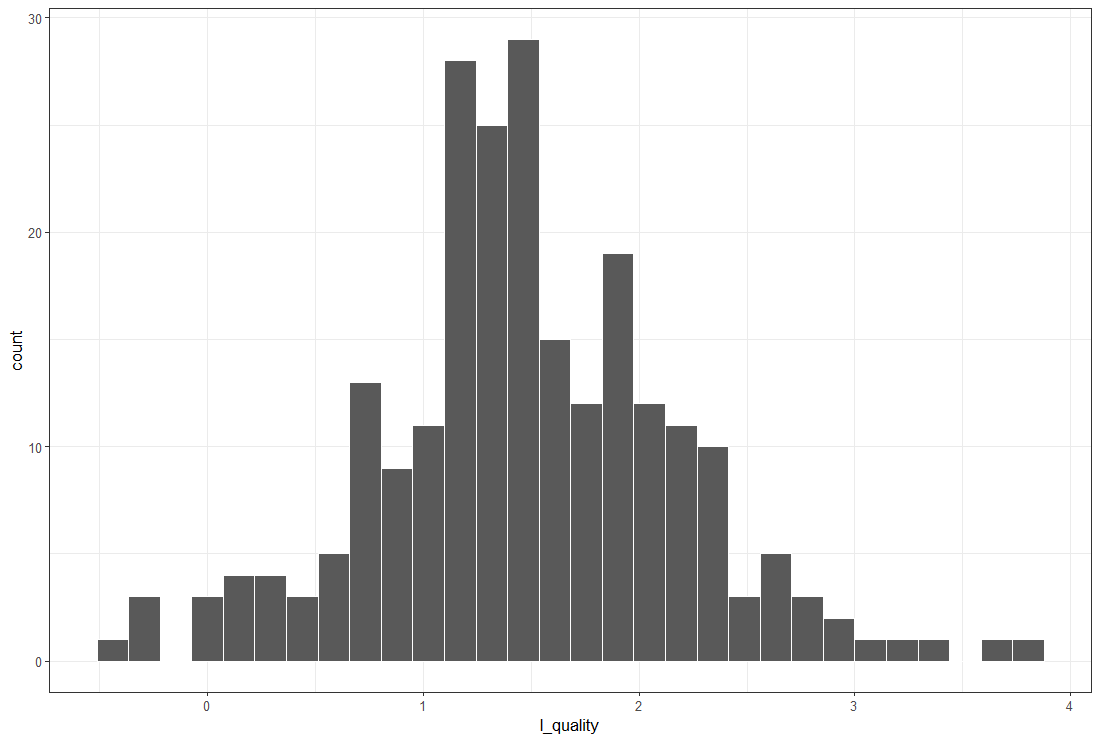
左右対称っぽい分布ですね。
年度ごとの平均値をみてみましょう。
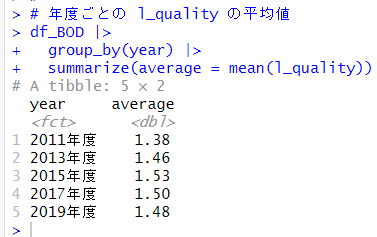
これら年度別の平均値が統計学的に有意な違いなのかどうか、これをシミュレーションベースの推定で確認します。
infer パッケージを使います。

Tidy ANOVA (Analysis of Variance) with infer • infer
こちらのサイトにやり方が書いてあるので、順を追って実行します。
まず、箱ひげ図を描きましょう。

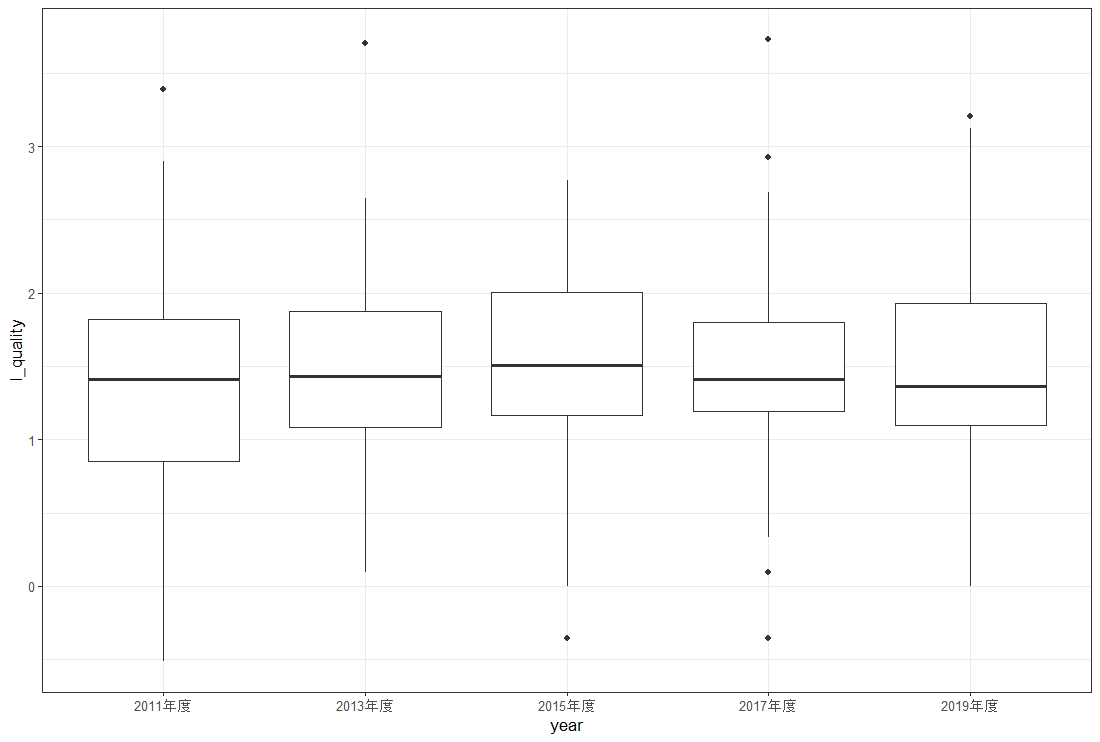
この箱ひげ図を見るかぎり、年度別の違いは無いようです。
次は、F 値を計算します。

F 値は 0.306 です。
次は、何度も何度も元のデータをかき混ぜてランダムな分布を作ります。

こうして作成した、ランダムな F 値の分布をヒストグラムにします。

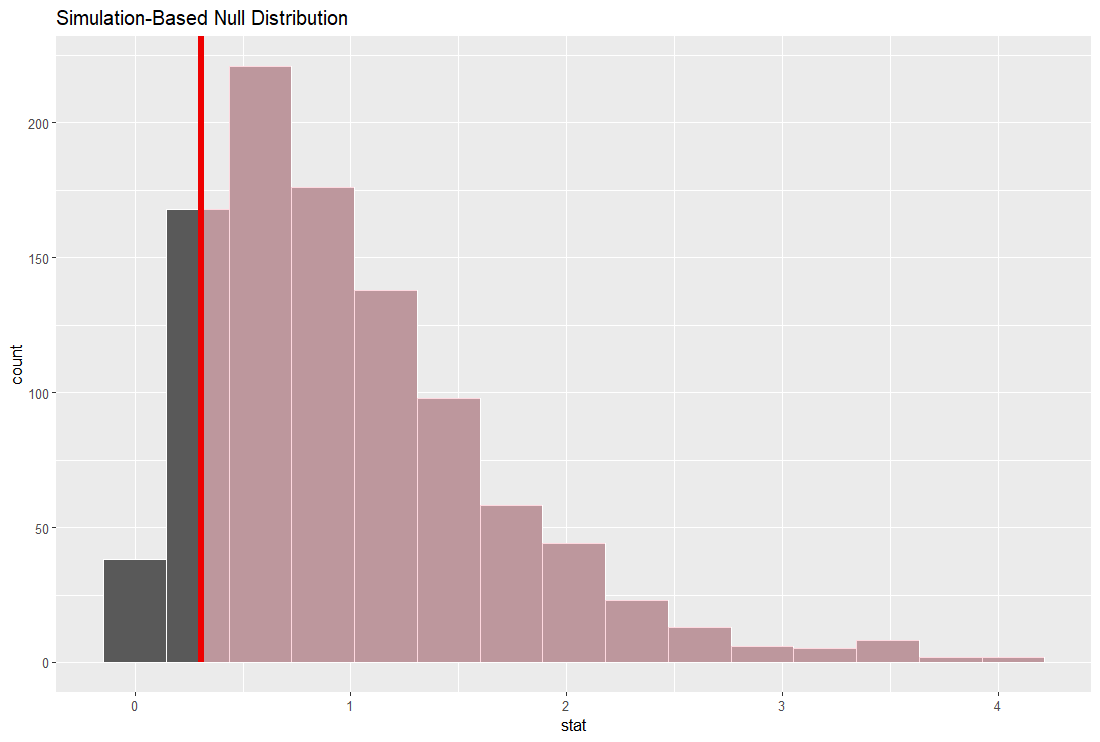
赤い垂線が実際の F 値です。これを見ると、実際の F 値はありふれた値ですね。つまり、year と l_quality には特別な関係性は無い、ということです。
理論的な F 値の分布も生成します。

これをグラフにします。

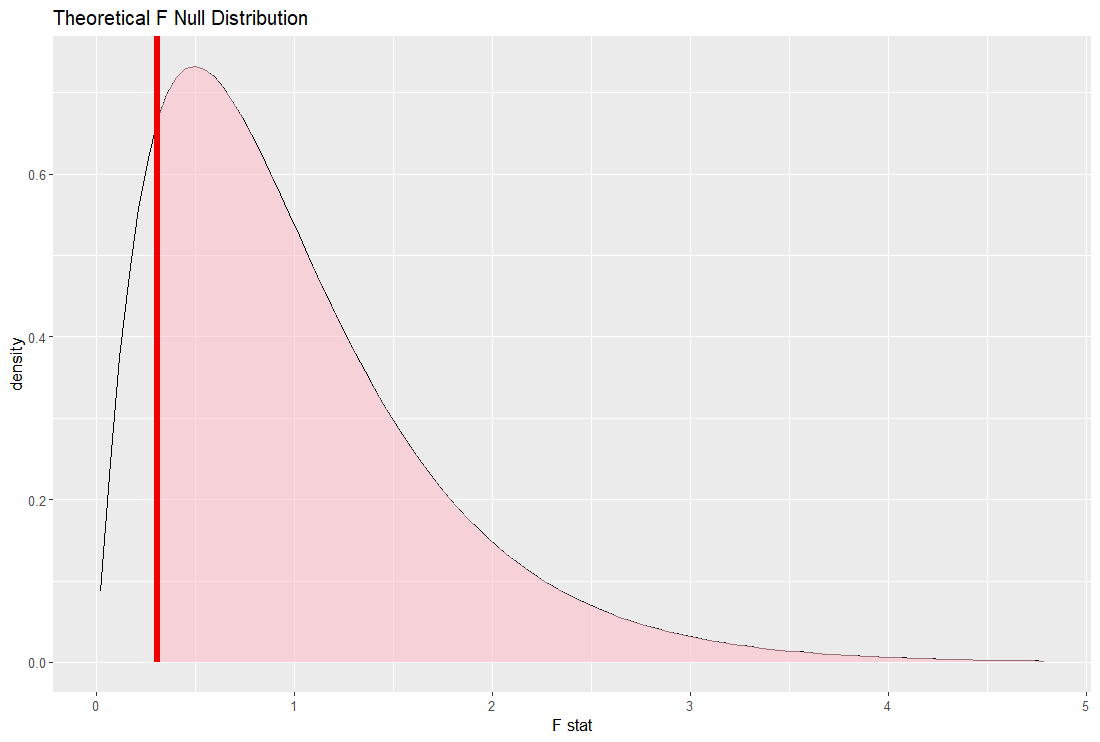
この理論ベースの F 値の分布に実際の F 値を重ねたグラフも同じような感じですね。
ランダムに生成した F 値と理論ベースの F 値を重ねるのは、visualize() 関数で、method = "both" にします。
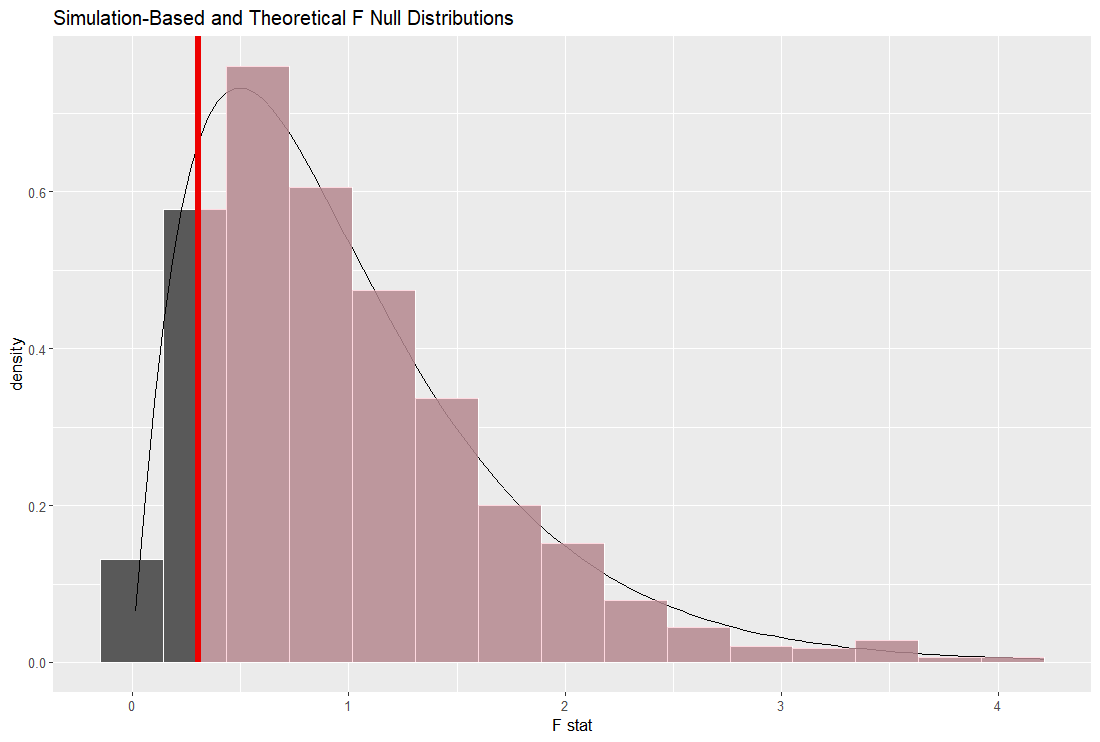
シミュレーションベースの F 値の分布から、実際の観測された F 値がでてくる確率、 p 値を計算します。

p 値は 0.879 です。つまり、l_quality は 年度によって違いが無い、という帰無仮説を棄却できません。l_quality は 年度によって違いがある、とは言えません。
今回は以上です。
次回は、
です。
初めから読むには、
です。