の続きです。
今回は一人当りの児童福祉費(ChildpM)を重回帰分析します。
説明変数は対数をとった面積(logArea)と対数をとった県内総生産(logGDP)です。
まずは、一番複雑なモデルから。

logArea:logGDPの交差項は不要のようです。削除します。

p値は0.9481です。model1もmodel2も有意な違いは無いです。より単純なmodel2を調べます。
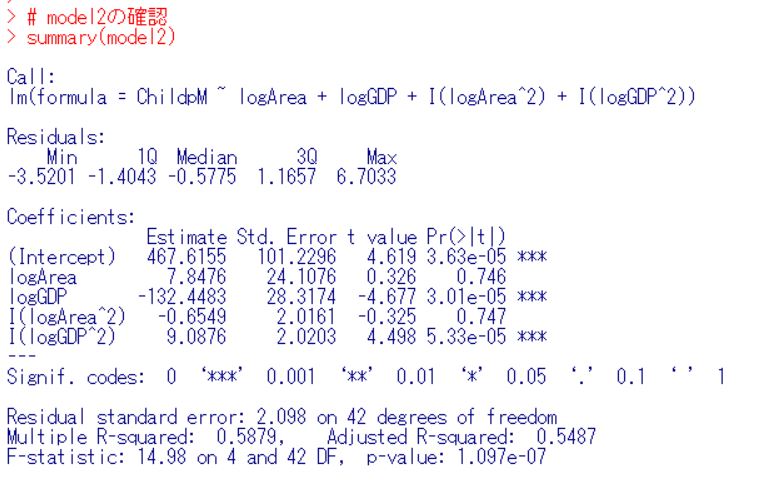
I(logArea^2)は不要ですね。削除します。

model2とmodel3では有意な違いはありません。model3をさらに調べます。
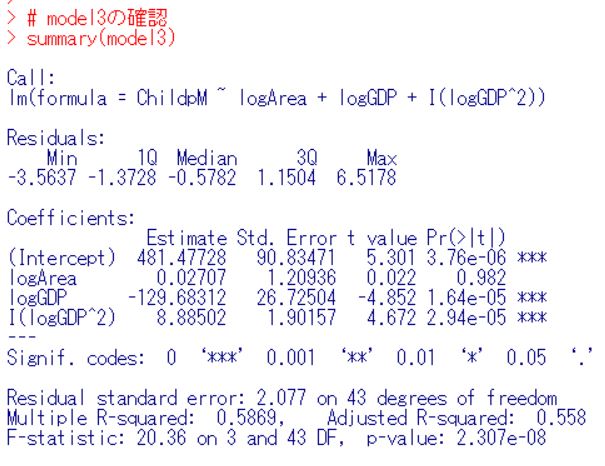
logAreaは不要ですね。削除します。前回の一人当り老人福祉費ではlogAreaは有意な変数でしたが、一人当りの児童福祉費では都道府県の面積は関係無いことがわかりました。

p値が0.9822です、model3とmodel4で有意な差はありません。
model4をみてみましょう。

これで、切片、logGDP、I(logGDP^2)の3つとも有意なモデルです。
logGDPをいろいろな値にして予測値を算出してみます。

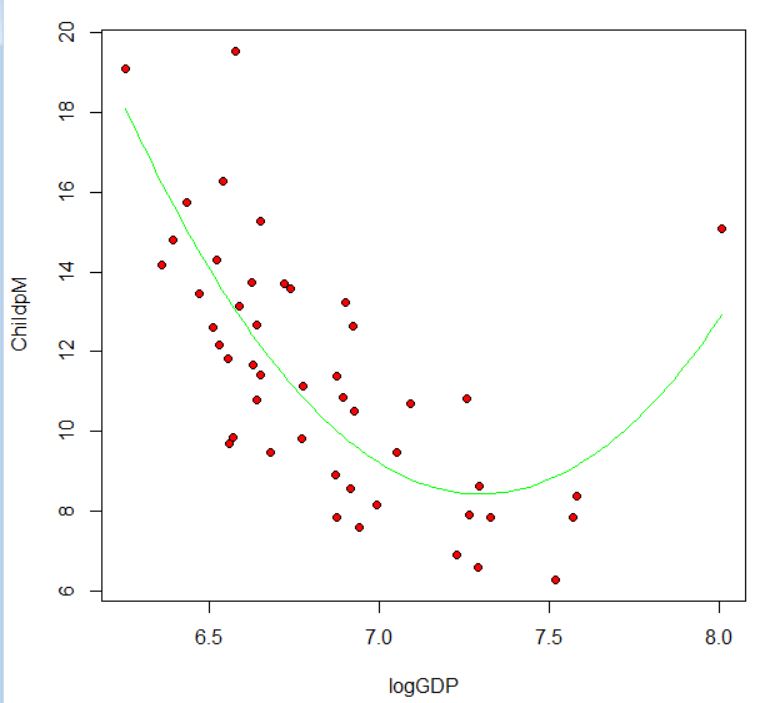
こうなりました。散布図の一番右端の点、東京都ですがこれが影響して回帰曲線が放物線状になっていますね。東京都を除外すれば、単純に直線になるのではないでしょうか?やってみましょう。

まずは、上のようにして東京都を除外したベクトルを作成しました。
後は同じ手順です。まずは一番複雑なモデルからやりましょう。

exTArea:exTGDPはいらないです。削除します。

exTm2を採用します。

I(exTArea^2)は不要ですね。

exTm3を採用します。

exTAreaは必要ないようです。

exTm4を採用します。

これで、切片、exTGDP、I(exTGDP^2)の3つが有意になりました。2乗項も残りましたね。散布図と回帰曲線を描きましょう。

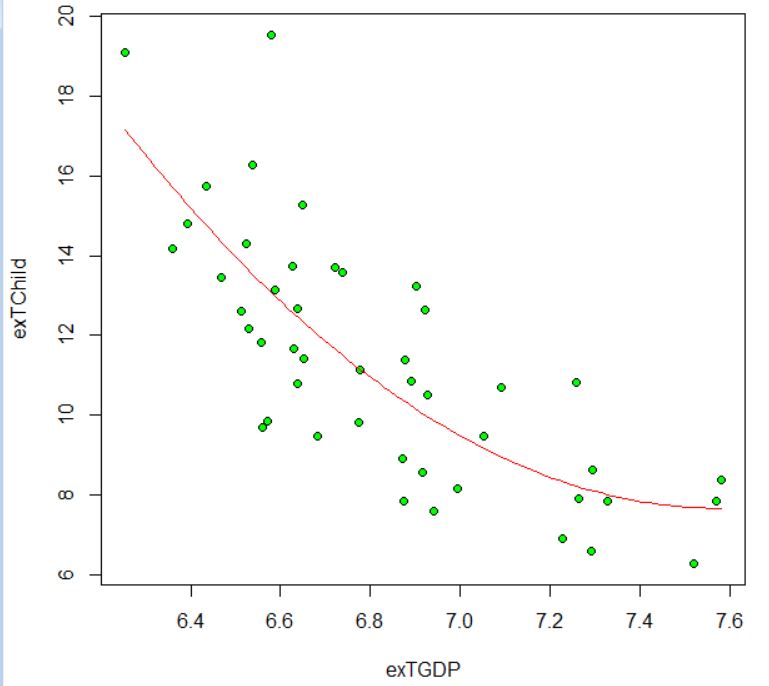
最後に東京都有りの散布図と回帰曲線、東京都無しの散布図と回帰曲線を並べて描いてみます。

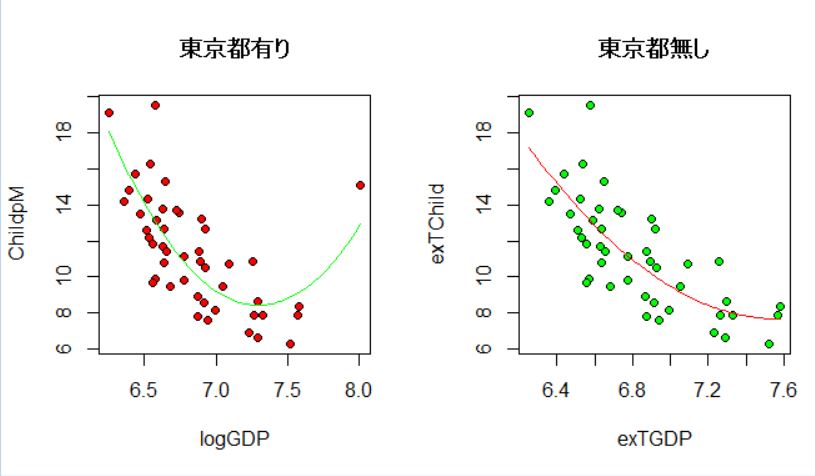
東京都を入れないほうが回帰曲線のあてはまりがいいようです。
実際に東京都有りのmodel4のAdjusted R-squaredは0.5681
東京都無しのexTm4のAdjusted R-squaredは0.6873と東京都無しのほうが高いです。
今回は以上です。