の続きです。
今回は、Touout(1人当りの一般事業投資額)を反応変数にして、説明変数をNonout(通学も従業もしていない人口の割合), Salaout(1人当りの給料・俸給), Zaiout(1人当りの財産所得, Shoout(1人当りの県民所得)を説明変数にして回帰分析をしたいと思います。
これらの変数は、前回の分析で外れ値の都道府県(東京都、岩手県、宮城県、福島県)を除外してあります。
lm関数で回帰分析をします。
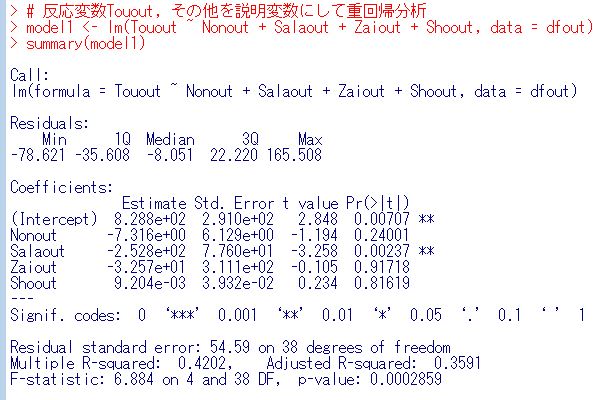
Zaioutは削除してもよさそうです。

update関数でmodel1からZaioutを削除したmodel2を作成し、anova関数でmodel1とmodel2を比較しています。p値は0.917なのでmodel1とmodel2に有意差はありません。
model2を見てみましょう。

Shooutを削除します。

Shooutを削除したmodel3とmodel2をanova関数で比較しています。p値は0.8284なので有意な違いはありません。model3を見てみましょう。

Nonoutを除外します。

model3とmodel4では有意な違いは無いです。model4を見てみます。

model4のp値は5.735e-06と0.05よりも小さいので有意なモデルです。Intercept, Salaoutの係数についてのp値も0.05以下です。
Touout = 494.44 - 197.30 x Salaout
というモデル式ですね。Salaoutが1(百万円)増えると、197.30(千円)減るということですね。1人当たりの給料・俸給が百万円増えると、1人当りの一般事業投資額は19万7300円減るということです。
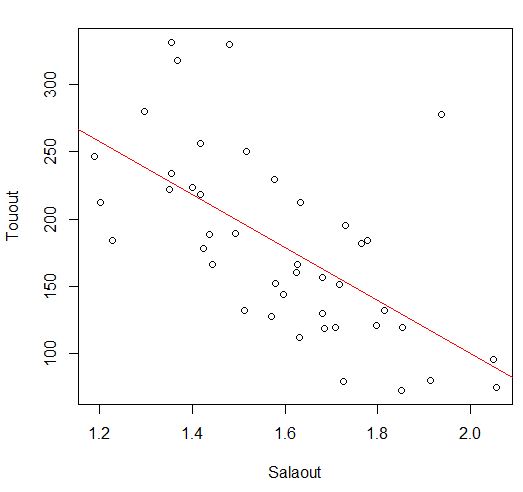
最後にTououtとSalaoutの散布図と回帰モデルの直線を描いて終わりましょう。