
Photo by K. Mitch Hodge on Unsplash
今回はKaggleのTitanicのデータを分析してみようと思います。生存・死亡を予測するのが目的ではなくて、単純にどんなデータなのか?というのを第一にしたいと思います。
まずは、Kaggleのウェブサイトからデータをダウンロードします。

https://www.kaggle.com/c/titanic/data
このサイトですね。このtest.csvが予測のテストのファイルで、train.csvが予測するモデルをトレーニングするファイルですね。分析にはRを使います。
とりあえず、何はさておきtidyverseパッケージを読み込んで、read_csv()関数でデータを読み込みます。


testとtrainで違うのは、testにはSurvived(生存=1, 死亡=0)の変数が無いことです。
この2つを合わせて分析したいので、testにSurvived = 2 として変数を追加しておきます。

trainとtestとを合体させます。rbind()関数かbind_rows()関数を使います。今回はtidyverseのbind_rows()を使います。
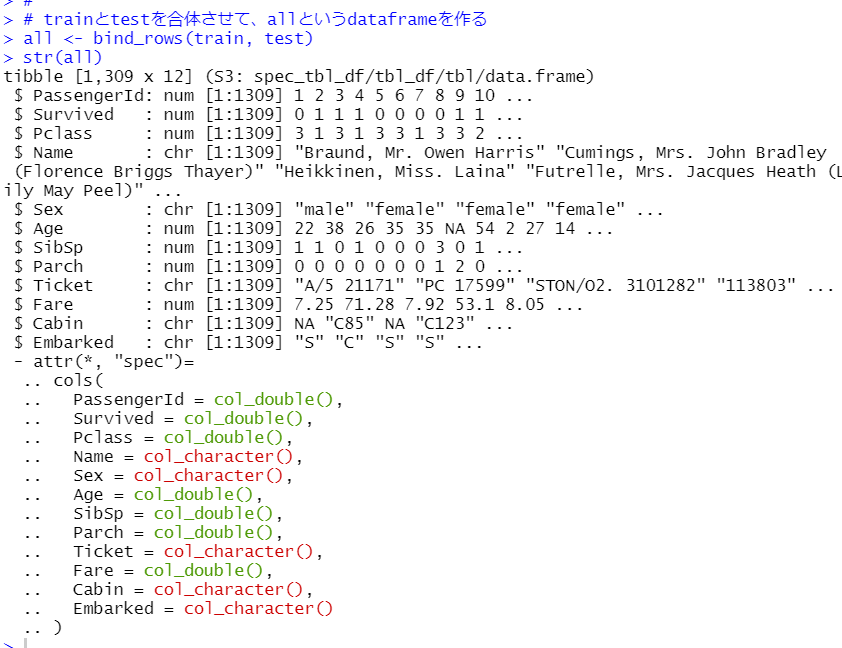
1309の観測、12の変数のデータフレームができました。
PassengerIdは乗客番号ですね。1番から1309番まで順番に付与されています。
1番から891番がtrain, 892番から1309番がtestのファイルです。あとあと、trainのデータ、testのデータと区別する必要がありそうなので、それぞれのインデックスを作っておきます。

それでは、一つ一つの変数を見ていきましょう。注意する点は、trainとtestで平均値や分散などのパラメータが違うのか、生存と死亡でパラメータが違うのか、です。
まずはPclassを見てみます。客室の等号ですね。1等客室、2等客室、3等客室の三つです。まずは、summary()関数を全体に使ってNAがあるのかどうか見てみます。

NAはありませんでした。平均値は2.295です。
train, testそれぞれの度数を見てみます。

train, testそれぞれの数が違うので単純な度数の比較では同じような度数なのか、違うような度数なのかよくわからないですね。prop.table()関数で比率にしてみます。

trainのほうは1等が24%, 2等が21%, 3等が55%ぐらいで、
testのほうは1等が26%, 2等が22%, 3等が52%でした。
この違いは統計的に有意なのでしょうか?
カイ二乗検定で確認します。

p-valueは0.6025なのでtrainとtestでPclassの度数分布に統計的に有意な違いは無いようです。
t.test()関数で平均値が同じかどうかのt検定をしてみます。

p-valueは0.3871なので平均値に違いは無いです。
wilcox.test()関数でウィルコクソンの順位和検定をしてみます。

p-valueは0.3577ですので両者の分布位置に違いは無いです。
以上からPclassはtrainとtestで違いがあるとは言えないことが確認できました。
Pclassは1, 2, 3と数値データですが、本質はファクターです。なので、Pclass = 3 をベースにして、Pclassが2のときに1を取るダミー変数、pc2とPclassが1のときに1を取るダミー変数pc1を作成します。

このpc1, pc2をexplanatory variablesに、Survivedをexplained variableにして回帰分析をしてみましょう。

Interceptの係数は0.24です。これは、Pclassが3の人、3等客室の人は24%の生存率です。
pc1は0.38727なので、1等客室の人の生存率は0.24236 + 0.38727 = 63%になります。
pc2は0.23046なので、2等客室の人の生存率は0.24236 + 0.23046 = 47%になります。
今回は以上です。
次回は
です。