
UnsplashのArham Jainが撮影した写真
の続きです。前回は、l_total: 建築物リフォーム・リニューアルの金額の自然対数値をl_shotoku23: 県民1人当たり所得とyear: 調査年度の2つの説明変数で回帰分析してみました。
今回は、前年度のl_totalも説明変数に加えて調査してみます。
まずは、分析のためのデータフレームを準備することからはじめます。
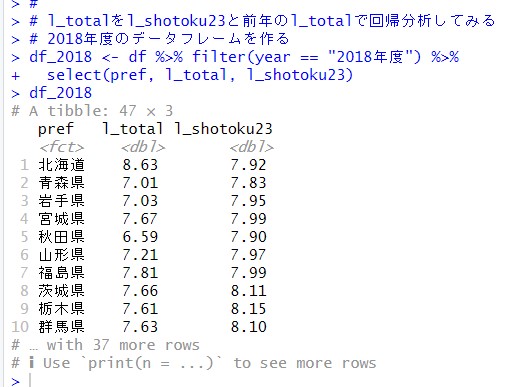
2018年度だけのデータフレームを作って、df_2018と名付けました。

2017年度だけのデータフレームを作って、df_2017と名付けました。

2016年度だけのデータフレームを作ってdf_2016と名付けました。
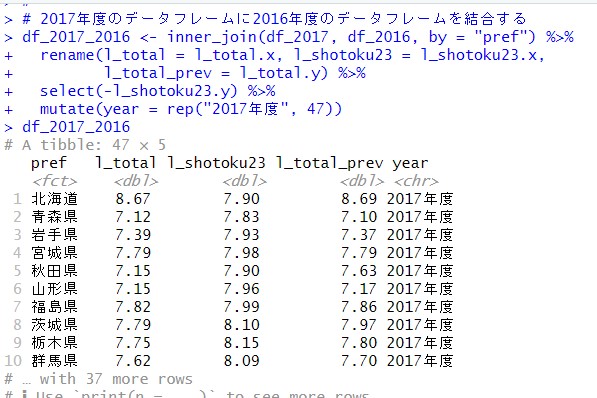
df_2017とdf_2016をinner_join()関数を使って結合しています。2016年度のl_totalの変数名をl_total_prevと変更しています。これは、2017年度から見たら、2017年のl_totalは前年度のl_totalだからです。このデータフレームをdf_2017_2016と名付けました。
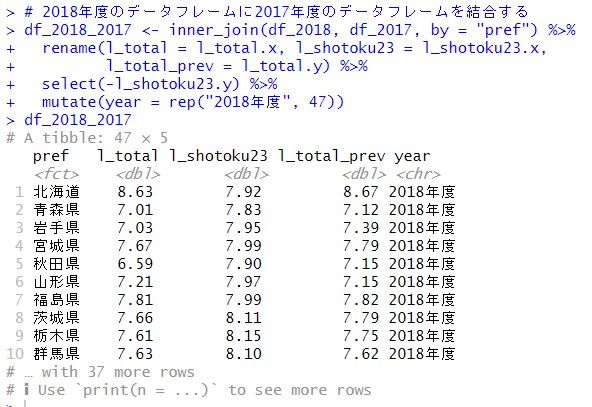
同じようにして、df_2018とdf_2017を結合しました。
そして、この2つのデータフレームをrbind()関数で縦方向に結合します。
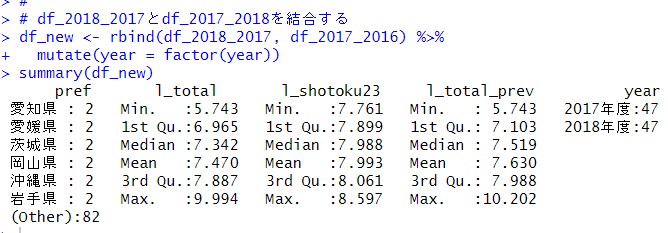
新しいdf_newというデータフレームができました。年度は、2017年度と2018年度だけです。2016年度は、前年度のl_totalがありませんので当然ですね。
これで、回帰分析のためのデータフレームが整いました。
回帰分析をlm()関数でやってみます。
![]()
summary()関数で回帰分析の結果をみてみます。

なんと、前年度のl_totalを説明変数に加えると、l_shotoku23はp値は0.164となりました。係数は0.41444ですが、統計的に有意とは言えないです。
回帰分析は、残差の2乗(=残差の分散)が説明変数と無関係、均一分散していないといけません。
確認してみます。
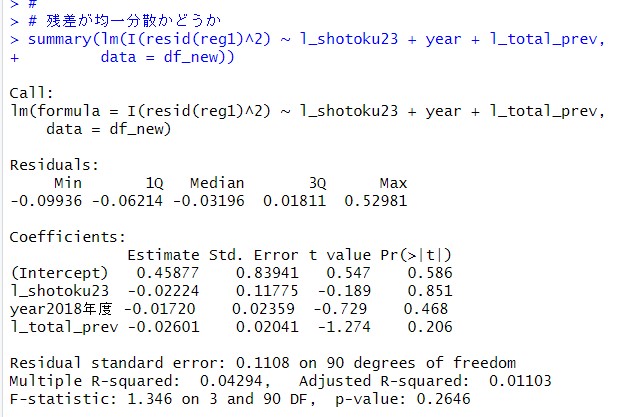
残差は、resid()関数で求めることができます。l_shotoku23, year, l_total_prevともに残差の2乗とは無関連なので、この回帰分析は問題ないです。
前回作成したmodel2でも残差の2乗が均一分散しているか確認しましょう。
model2はこのような、l_shotoku23とyearが説明変数でした。l_shotoku23の係数は4.0380で有意でした。
今回のモデルのreg1のl_shotoku23の係数は0.4ぐらいですから10倍も大きいですね。
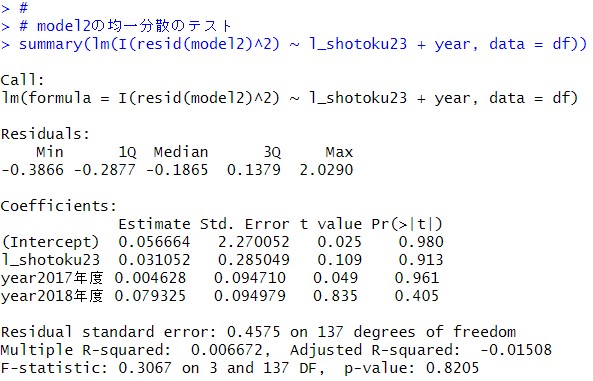
model2も残差は、均一分散しているようです。
今回は以上です。
次回は、
です。
初めから読むには、
です。