
(Bing Image Creator で生成: プロンプト: Close up photograph of Cornus florida flowers, the tree is standing on the top of high mountains, photo)
の続きです。
今回も Wooldridge の Introductory Econometrics: A modern Approach, 7eを教科書にして回帰分析をしてみます。
今回は37ページ目から始まっている2-4b Incorporating Nonlinearities in Simple Regressionの部分をやります。ここでは説明変数、被説明変数を対数変換したら、モデル式はどういう解釈になるか、ということが書かれています。
はじめはlevel -level モデルです。これは前回と同じモデルで、説明変数も被説明変数もそのままの値のモデルです。
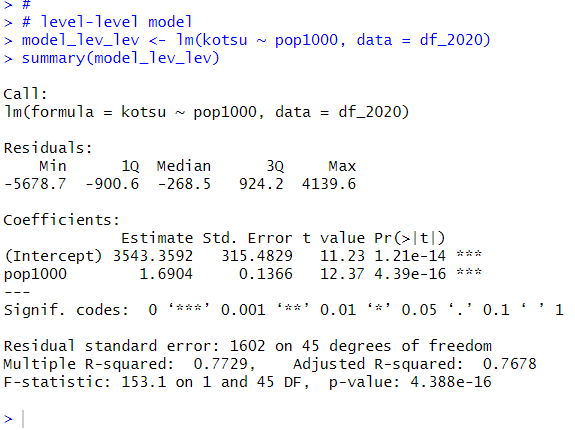
kotsu = 3543 + 1.69 * pop1000 + u
という式になります。これは、pop1000が1上がったら、kotsuが1.69増える、という解釈ですね。Δkotsu = 1.69 * Δpop1000です。pop1000 = 1ということは、1000人です。人口が1000人増えたら、交通量は1.69台増える、ということです。これは特に
次はlevel - log モデルです。
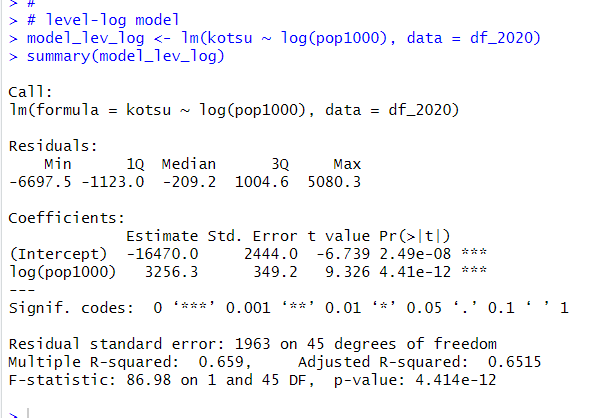
kotsu = -16470 + 3256 * log(pop1000) + u です。
Δkotsu = 3256 * Δlog(pop1000) です。これは式を変形すると、
Δkotsu = (3256 / 100) * %Δpop1000 になります。もう少し式を変形すると、
Δkotsu = 32.56 * %Δpop1000 になります。pop1000が1%増えると、kotsuが32.56台増える、ということです。これは本当にそうなのか検証の必要がありますね。
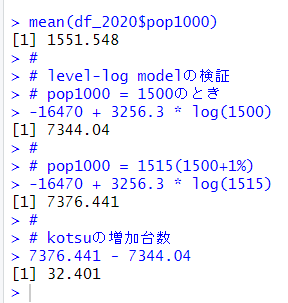
pop1000の平均値が1551.548なので、pop1000 = 1500でやってみました。
pop1000 = 1500 のとき、kotsu = 7344.04台でした。
1500の1%増えた値、pop1000 = 1515にしたとき、kotsu = 7376.441台でした。
なので、kotsuの増加は、7376.441 - 7344.04 = 32.401となりました。
モデルは32.56台増えるという解釈なので、ほぼ一致してます。
次は、log-levelモデルです。
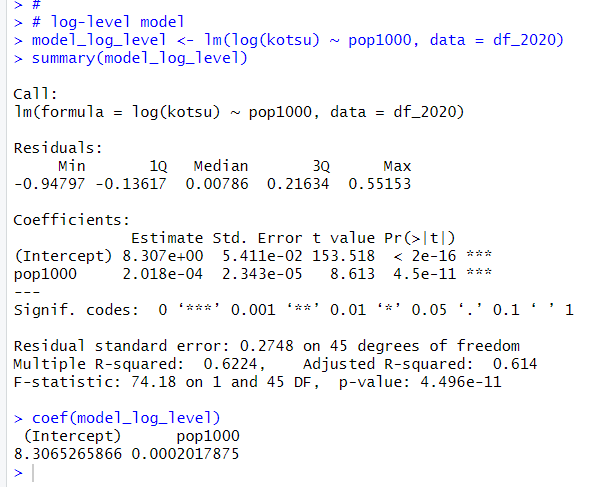
log(kotsu) = 8.3065 + 0.0002017875 * pop1000 + u です。
これは、Δlog(kotsu) = 0.0002017875 * Δpop1000 です。この式を変形すると、
%Δkotsu = 100 * 0.0002017875 * Δpop1000 です。式をさらに変形すると、
%Δkotsu = 0.02017875 * Δpop1000 です。pop1000が1増えると、kotsuが0.02017875%増える、という解釈です。これも検証が必要ですね。

pop1000 = 1500 のとき、kotsu = 5481.904で、pop1000 = 1501 のとき、kotsu = 5483.01でした。増加率は0.02017547%です。検証できました。
そして、最後はlog-log modelです。
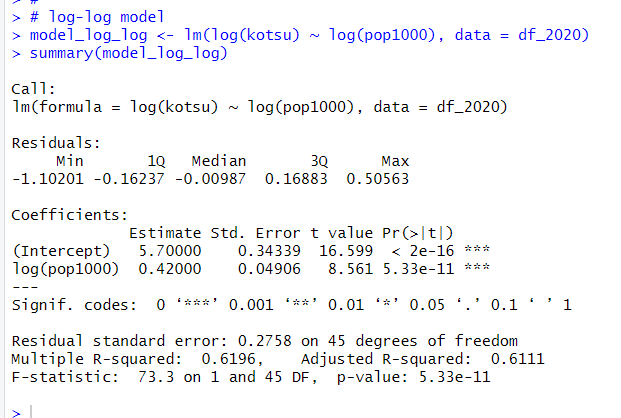
log(kotsu) = 5.7 + 0.42 * log(pop1000) + u です。
これは、Δlog(kotu) = 0.42 * Δlog(pop1000)です。式を変形すると。
%Δkotsu = 0.42 * %Δpop1000 です。pop1000が1%増えると、kotsuは0.42%増える、という解釈です。検証してみましょう。

pop1000 = 1500 のとき、kotsu = 6448.008です。pop1000 = 1515のとき、kotsu = 6475.012です。kotsuは0.418796%増えました、ほぼ0.42%ですね。検証できました。
今回は以上です。
次回は
です。
初めから読むには、
です。
今回のコードは以下になります。
#
# level-level model
model_lev_lev <- lm(kotsu ~ pop1000, data = df_2020)
summary(model_lev_lev)
#
# level-log model
model_lev_log <- lm(kotsu ~ log(pop1000), data = df_2020)
summary(model_lev_log)
#
# level-log modelの検証
# pop1000 = 1500のとき
-16470 + 3256.3 * log(1500)
#
# pop1000 = 1515(1500+1%)
-16470 + 3256.3 * log(1515)
#
# kotsuの増加台数
7376.441 - 7344.04
#
# log-level model
model_log_level <- lm(log(kotsu) ~ pop1000, data = df_2020)
summary(model_log_level)
coef(model_log_level)
#
# log-levelの検証
# pop1000 = 1500のとき
predict(model_log_level, newdata = data.frame(pop1000 = 1500)) |>
exp()
#
# pop1000 = 1501のとき
predict(model_log_level, newdata = data.frame(pop1000 = 1501)) |>
exp()
#
(5483.01 / 5481.904 - 1) * 100
#
# log-log model
model_log_log <- lm(log(kotsu) ~ log(pop1000), data = df_2020)
summary(model_log_log)
#
# log-log modelの検証
# pop = 1500のとき
predict(model_log_log, newdata = list(pop1000 = 1500)) |>
exp()
#
# pop = 1515のとき
predict(model_log_log, newdata = list(pop1000 = 1515)) |>
exp()
#
(6475.012 / 6448.008 - 1) * 100
#