
(Bing Image Creatorで生成: プロンプト: close-up photo of Viola mandshurica flowers, flowering small country road, photo)
の続きです。今回からしばらくは、
Introductory Ecnometrics: A Modern Approach を参考書にして、計量経済学的な分析をしてみたいと思います。
私が持っているのは、Seventh Edition(ISBN: 987-1-337-55886-0)です。
kotsu: 道路平均交通量を被説明変数にして、pop: 人口を説明変数にした単回帰モデルを考えます。
kotsu = beta0 + beta1 * pop + u
というモデルです。uは誤差項です。
はじめは、2020年度のデータだけで分析してみます。
lm()関数を使います。

係数が1.690e-03と少しわかりにくい表示になってしまいました。
popは【人】単位なので、【千人】単位にして、それをつかって回帰分析します。

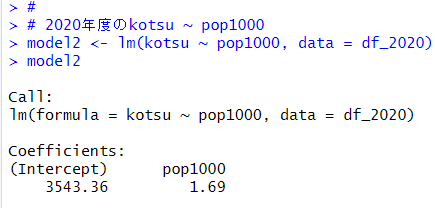
kotsu = 3543 + 1.69 * pop1000 + u
という回帰式が推定されました。人口が千人増えると、交通量は1.69台増えるという式の意味です。
summary()関数でモデルのサマリーをみてみます。
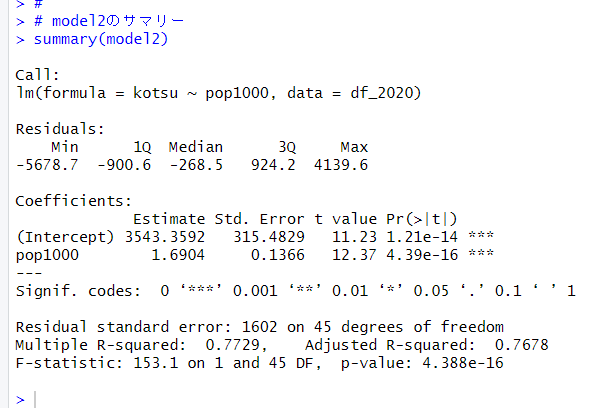
pop1000のp値は4.39e-16と非常に小さい値です。
Wooldridge(7e)の26ページ目の[2.19]の計算式はbeta1を算出する計算式があります。
(sum(xi - xbar)(yi - ybar)) / sum*1 * (kotsu - mean(kotsu))) /
sum*2^2)
)
#
# beta0 の算出
beta1 <- df_2020 |>
summarize(
beta1 = sum*3 * (kotsu - mean(kotsu))) /
sum*4^2)
) |>
pull()
beta1
#
beta0 <- df_2020 |>
summarize(
beta0 = mean(kotsu) - beta1 * mean(pop1000)) |>
pull()
beta0
#
# SSTの計算
SST <- sum*5^2)
SST
#
# SERの計算
SSE <- sum*6^2)
SSE
#
# SSRの計算
SSR <- sum(resid(model2)^2)
#
# SST = SSE + SSR の確認
SST
SSE + SSR
#
# R2の算出
R2 = SSE / SST
R2
R2 = 1 - SSR / SST
R2
#
*1:xi - xbar)^2)
という式です。
Rでこの式を再現してみます。

1.69とlm()関数での結果と同じになりました。
beta0は[2.17]の式に
beta0 = yabr - beta1*xbar とあります。同じように、Rで計算してみます。

beta0は3543.359となりました。lm()関数との結果と同じですね。
続いて、Wooldridge(7e)の34ページ目にある、total sum of squares(SST), explained sum of squares(SSE) and residual sum of squares(SSR)を計算します。
SST = sum((yi - ybar)^2) [2.33]
SSE = sum((yi_hat - ybar)^2) [2.34]
SSR = sum(u_hat^2) [2.35]
という計算式です。yi は実際のkotsu, yi_hatは回帰式で推定したkotsu, y_barはkotsuの平均値、u_hatは回帰式から計算された残差です。

yi_hatはfitted(model2)で、u_hatはresid(model2)で算出できます。
そして、SST = SSE + SSR [2.36] が成り立るとWooldrife(7e)には書いてあります。
被説明変数の変動 = 推定された被説明変数の変動 + 残差の変動 という意味ですかね。
たしかめます。

確かに、SST = SSE + SSRでした。
そして、35ページ目に
R2 = SSE / SST = 1 - SSR / SST [2.38]
とR-squaredの計算式があります。これも確認します。

どちらの計算方法でも0.7728722です。そしてこれは、summary()関数でのR-squaredの値と同じですね。
今回は以上です。
次回は
です。
初めから読むには、
です。
今回のコードは以下になります。
#
# 2020年度のkotsu ~ popのモデル
model1 <- lm(kotsu ~ pop, data = df_2020)
model1
#
# popを千人単位に変更する
df_2020 <- df_2020 |>
mutate(pop1000 = pop / 1000)
#
# 2020年度のkotsu ~ pop1000
model2 <- lm(kotsu ~ pop1000, data = df_2020)
model2
#
# model2のサマリー
summary(model2)
#
# beta1の算出
df_2020 |>
summarize(
beta1 = sum((pop1000 - mean(pop1000
*2:pop1000 - mean(pop1000
*3:pop1000 - mean(pop1000
*4:pop1000 - mean(pop1000
*5:df_2020$kotsu - mean(df_2020$kotsu
*6:fitted(model2) - mean(df_2020$kotsu
