
Photo by Ray Hennessy on Unsplash
の続きです。
前回は、単回帰分析で SST(total sum of squares) = SSE(explained sum of squares) + SSR(residual sum of squares)などの関係をみてみました。
今回は、Gdp, Edを対数変換して回帰分析してみます。
level - level : Gdp = beta_0 + beta_1 * Ed + u
log - level : log(Gdp) = beta_0 + beta_1 * Ed + u
level - log : Gdp = beta_0 + beta_1 * log(Ed) + u
log - log : log(Gdp) = beta_0 + beta_1 * log(Ed) + u
の4つの形態の回帰分析モデルを考えてみます。
まず、level - level のモデル、これは前回と同じですね。

Gdp = -6050 + 4.744 * Ed + u
というモデルです。これは、Edが1増えたら、Gdpは4.744( = beta_1) 増えるということですね。
predict()関数を使って、 Ed = 10000 のときと Ed = 10001 のときのGdpの値を確認してみます。
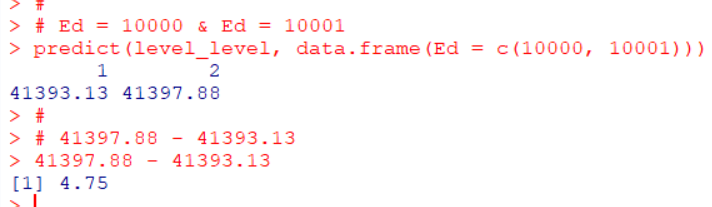
4.75 増えています。
次は、log(Gdp) = beta_0 + beta_1 * Ed + u
という log - level モデルです。
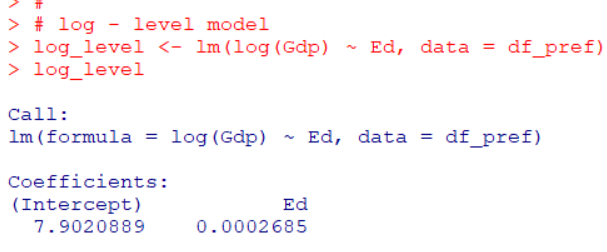
log(Gdp) = 7.90 + 0.0002685 * Ed + u
というモデルです。
これは、Edが1増えたら、Gdpが0.0002685%( = beta_1%) 増える、ということです。
確かめてみます。
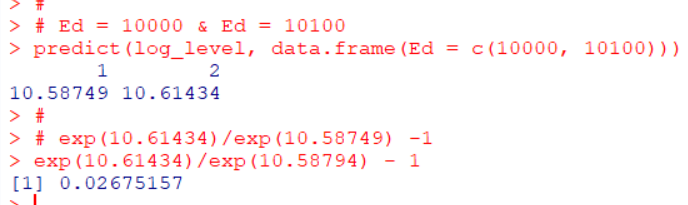
0.0268%増えました。
3番目は、level - log model
Gdp = beta_0 + beta_1 * log(Ed) + u
です。

Edが1%増えると、Gdpは183.74( = beta_1/100%)増えるということです。
確かめてみましょう。
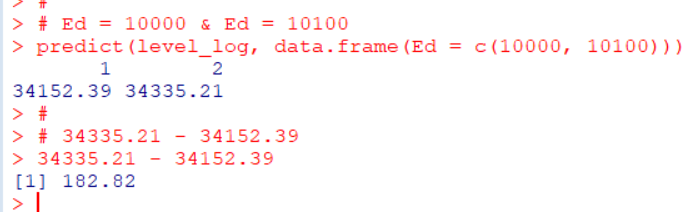
183ぐらい増えました。
最後のモデルは log - log model です。
log(Gdp) = beta_0 + beta_1 * log(Ed) + u
です。
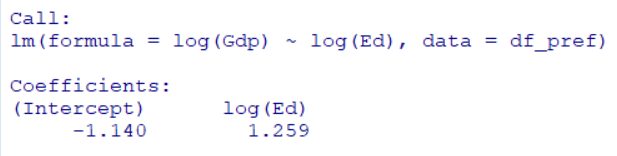
log(Gdp) = -1.140 + 1.259 * log(Ed) + u
です。これは、Edが1%増えれば、Gdpは1.259( = beta_1)%増えるということです。
確かめてみます。
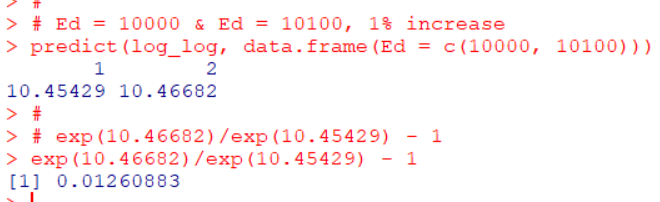
0.0126, つまり1.26%増えています。
この4つをまとめます。
level - level : 説明変数が1増えると、被説明変数はbeta_1だけ増える
log - level : 説明変数が1増えると、被説明変数はbeta_1*100%だけ増える
level - log : 説明変数が1%増えると、被説明変数はbeta_1/100だけ増える
log - log : 説明変数が1%増えると、被説明変数はbeta_1%だけ増える
となります。
4つのモデルの散布図を描きます。

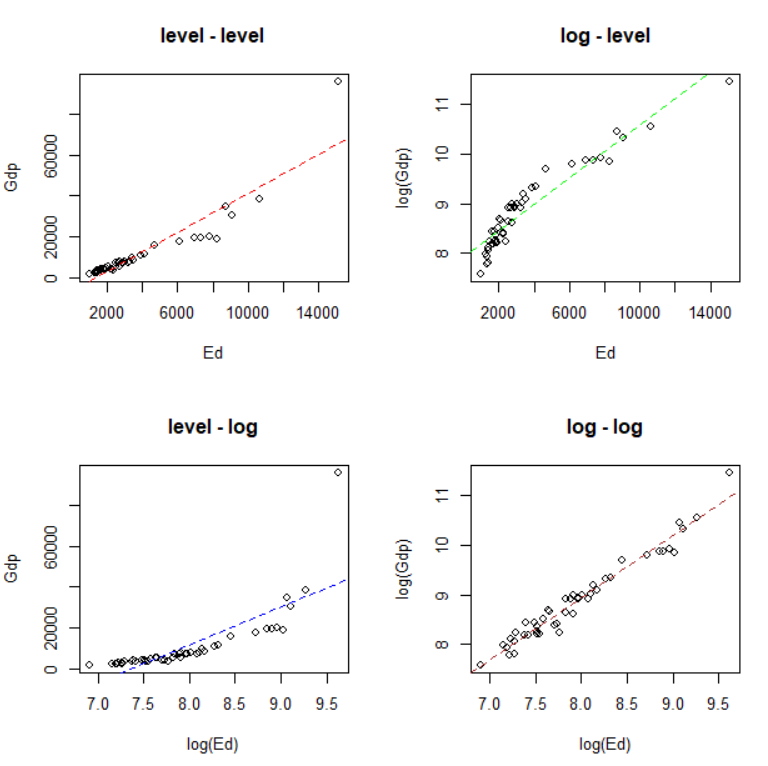
log - log model が一番フィットしている感じです。
各モデルのR2を確認します。
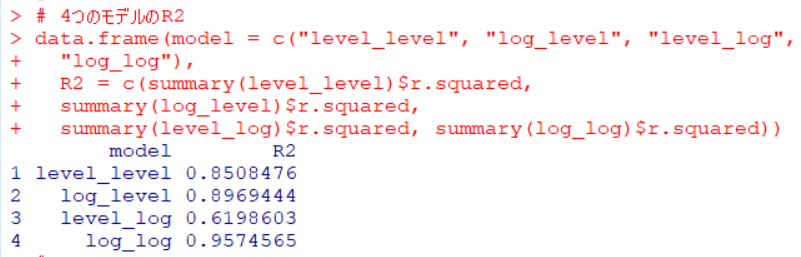
log_log model のR2が0.957と一番大きいです。
log - log model は
log(Gdp) = -1.140 + 1.259 * log(Ed) + u
というモデルです。Ed: 教育費が1%増えれば、Gdp: 県内総生産額が1.259%増える、という回帰式です。
今回は以上です。
次回は
です。
初めから読むには、
です。