の続きです。
今回は年代と退院済フラグでクロス表を作成します。
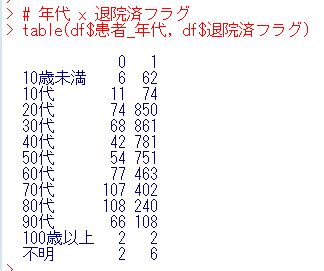
年代の不明を削除して、100歳以上を90代と一緒にして、90代以上にしましょう。

クロス表を作成します。

prop.table関数で比率をみてみます。

年代が上がるほど、退院済フラグが0の比率が高くなっています。
chisq.test関数でカイ二乗検定をしてみます。

p-value < 2.2e-16と0.05よりも小さいですから、年代と退院済フラグは関連性があります。
年代が上がるほど退院済フラグが0の比率が高く、逆に言えば退院済フラグが1の比率が低くなっていますので、
を参考にして、Proportion Dataの分析をしてみます。
まず、年代x退院済フラグの1列目と2列目をresponse variablesにします。

次にexplanatory variableを用意します。10歳未満を5, 10代を15, 20代を25、というようにしましょう。

plot関数で横軸に年代, 縦軸に退院済フラグが0の比率のグラフを描いてみます。


glm関数で回帰分析をしてみます。

x の係数の符号はプラスです。xが大きくなるほど、yの比率は大きくなるということですね。
さきほどの散布図にモデルの予測値を追加してみます。


10代未満から20代のフィットが今一つですね。
xの2乗項を追加したモデルを試してみます。

anova関数で、model1とmodel2を比較しました。model1とmoel2は有意に違います。
そして、model2のほうがResid. Devが小さいのでよさそうです。
summary関数で見てみましょう。

xの2乗項も係数のp値は0.05以下で有意です。AICは86.662とmodel1の143.64よりも小さいです。
散布図にmodel1の予測値、model2の予測値を重ねて描きましょう。


model2のほうがフィットしています。
今回は以上です。
